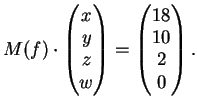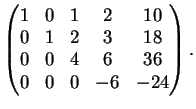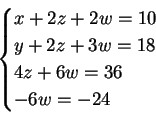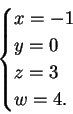Next: Indice
Up: Esercizi
Previous: Geometria 20 giugno 2000.
Indice
Domande.
- Siano
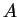 e
e 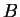 due matrici
due matrici
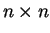 a coefficienti reali.
Il determinante della matrice prodotto
è uguale a
a coefficienti reali.
Il determinante della matrice prodotto
è uguale a
- Siano
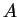 e
e 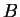 due matrici
due matrici
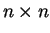 a coefficienti reali.
Il determinante della matrice somma
è uguale a
a coefficienti reali.
Il determinante della matrice somma
è uguale a
- Siano
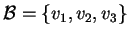 una base di
una base di 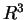 .
L'insieme:
.
L'insieme:
- Sia
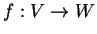 una applicazione lineare e iniettiva.
Siano
una applicazione lineare e iniettiva.
Siano
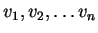 in
in 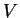 vettori linearmente indipendenti.
I vettori:
sono
vettori linearmente indipendenti.
I vettori:
sono
- Siano
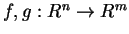 applicazioni lineari
e sia
applicazioni lineari
e sia 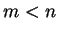 . Esistono vettori non nulli sui quali
. Esistono vettori non nulli sui quali 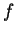 e
e 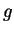 coincidono?
coincidono?
- Sia
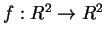 una applicazione lineare di matrice
Risulta:
una applicazione lineare di matrice
Risulta:
- Sia
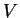 uno spazio vettoriale e
uno spazio vettoriale e 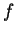 l'endomorfismo di
l'endomorfismo di 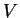 definito da
L'endomorfismo
definito da
L'endomorfismo 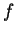 è diagonalizzabile
è diagonalizzabile
- Sia
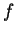 un endomorfismo di uno spazio vettoriale e siano
un endomorfismo di uno spazio vettoriale e siano 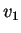 e
e 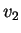 due
autovettori relativi ad autovalori distinti.
Il vettore
due
autovettori relativi ad autovalori distinti.
Il vettore
- Siano
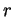 e
e 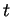 due rette incidenti e sia
due rette incidenti e sia 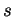 una retta incidente
una retta incidente 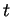 .
Le rette
.
Le rette 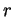 ed
ed 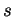 sono
sono
- Siano
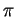 un piano e
un piano e 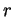 una retta ortogonale a
una retta ortogonale a 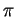 . Sia
. Sia
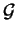 il fascio di piani per
il fascio di piani per 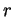 . Esistono piani di
. Esistono piani di
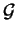 paralleli a
paralleli a 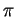 ?
?
Esercizi.
1) Discutere e trovare le soluzioni del seguente sistema :
al variare del parametro reale 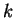 .
.
2) Sia 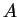 la matrice
la matrice
- Determinare autovalori e autospazi di
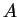 .
.
- Se possibile determinare una base di autovettori di
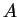 .
.
3) Sia 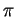 il piano di equazione
e sia
il piano di equazione
e sia 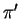 il piano per l'origine
il piano per l'origine 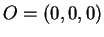 e ortogonale alla retta
e ortogonale alla retta
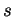 di equazioni
Dette
di equazioni
Dette 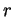 la retta di intersezione tra
la retta di intersezione tra 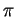 e
e 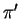 ed
ed 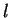 la retta di
equazioni parametriche
si studi la posizione reciproca di
la retta di
equazioni parametriche
si studi la posizione reciproca di 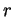 e
e 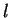 .
.
4) Sia
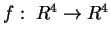 l'applicazione lineare definita da
l'applicazione lineare definita da
Scrivere la matrice di 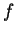 rispetto alla base canonica di
rispetto alla base canonica di 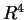 .
Provare che l'applicazione
.
Provare che l'applicazione 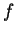 è invertibile e trovare la controimmagine di
è invertibile e trovare la controimmagine di
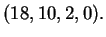
Soluzione
Esercizio 1.
La matrice completa associata al sistema è la matrice
Riducendola a gradino si ottiene :
Per
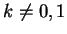 le matrici completa e incompleta associate al sistema hanno
entrambe rango
le matrici completa e incompleta associate al sistema hanno
entrambe rango 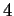 sicchè il sistema ha una unica soluzione:
Per
sicchè il sistema ha una unica soluzione:
Per 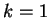 la matrice completa associata al sistema diventa:
Le matrici completa e incompleta associate al sistema hanno
entrambe rango
la matrice completa associata al sistema diventa:
Le matrici completa e incompleta associate al sistema hanno
entrambe rango 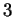 dunque il sistema ammette infinite soluzioni:
Infine per
dunque il sistema ammette infinite soluzioni:
Infine per 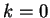 la matrice completa diventa
Riducendola ulteriormente si trova:
la matrice completa diventa
Riducendola ulteriormente si trova:
L'ultima riga della matrice corrisponde all'equazione (manifestamente falsa)
da cui segue che per 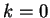 il sistema non ha soluzioni.
il sistema non ha soluzioni.
Esercizio 2.
Il polinomio caratteristico della matrice 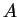 è:
è:
Gli autovalori di 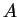 sono
sono 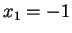 con molteplicità algebrica
con molteplicità algebrica 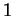 e
e 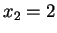 con
molteplicità algebrica
con
molteplicità algebrica 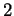 .
.
L'autospazio relativo all'autovalore 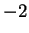 è
è
L'autospazio relativo all'autovalore 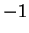 è
è
La matrice 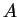 non è diagonalizzabile perchè
pertanto non si può trovare una base di autovettori di
non è diagonalizzabile perchè
pertanto non si può trovare una base di autovettori di 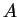 .
.
Esercizio 3
Il vettore direttore di 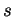 è
è
e quindi il piano 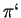 ha equazione
La retta
ha equazione
La retta 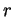 è pertanto
ossia:
Quindi le rette
è pertanto
ossia:
Quindi le rette 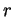 e
e 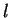 non sono parallele; non avendo punti in comune sono
allora sghembe.
non sono parallele; non avendo punti in comune sono
allora sghembe.
Esercizio 4
La matrice di 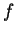 rispetto alla base canonica di
rispetto alla base canonica di 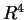 è:
è:
Riduciamo a scala 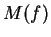 :
matrice ridotta di
:
matrice ridotta di 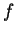 . È noto che
. È noto che
 , perciò
essendo
, perciò
essendo
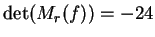 , è
, è
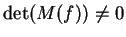 e quindi
e quindi 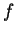 è invertibile.
è invertibile.
La controimmagine di
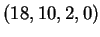 sarà pertanto costituita da un solo vettore, l'unica
soluzione del sistema
sarà pertanto costituita da un solo vettore, l'unica
soluzione del sistema
La matrice completa associata al sistema appena scritto è
che, ridotta a gardino, diventa
L'ultima matrice corrisponde al sistema:
che ammette l'unica soluzione
La controimmagine di
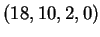 è quindi il vettore
è quindi il vettore
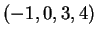 .
.




Next: Indice
Up: Esercizi
Previous: Geometria 20 giugno 2000.
Indice
Andreatta Marco
2000-09-18
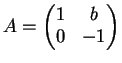
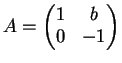
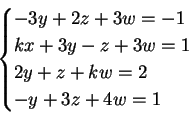
![]() la matrice
la matrice
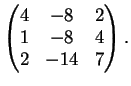
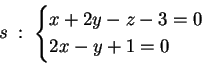
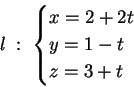
![]() l'applicazione lineare definita da
l'applicazione lineare definita da
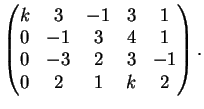
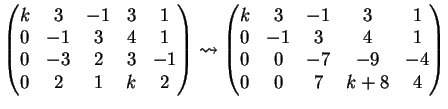
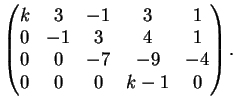
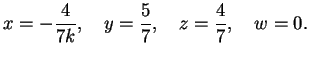
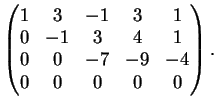
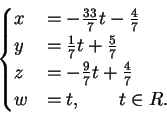
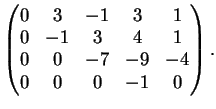
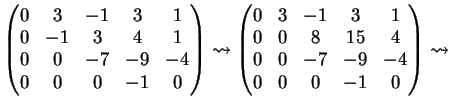
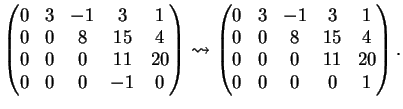
![]() è:
è:
![]() è
è
![]() è
è
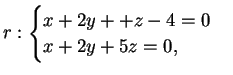
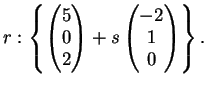
![]() rispetto alla base canonica di
rispetto alla base canonica di ![]() è:
è:
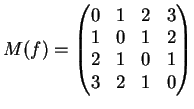
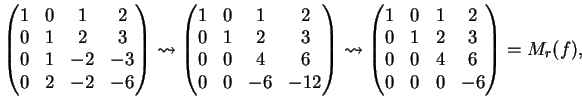
![]() sarà pertanto costituita da un solo vettore, l'unica
soluzione del sistema
sarà pertanto costituita da un solo vettore, l'unica
soluzione del sistema