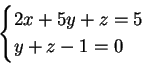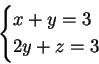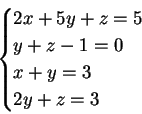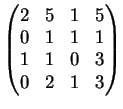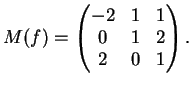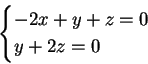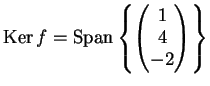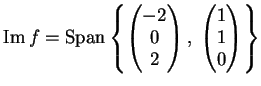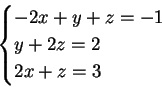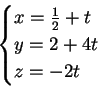Next: Geometria 2 marzo 1999.
Up: Esercizi
Previous: Geometria 8 febbraio. Tema
Indice
Rispondere, giustificando brevemente la risposta, ad almeno due delle
prime quattro domande e risolvere il maggior numero degli esercizi seguenti.
Domande.
- Dire se è vera la seguente affermazione.
Se  sono tre vettori linearmente indipendenti di uno
spazio vettoriale
sono tre vettori linearmente indipendenti di uno
spazio vettoriale  anche
anche
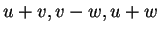 sono linearmente indipendenti.
sono linearmente indipendenti.
- Dire se è vera la seguente affermazione.
Siano
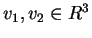 e
e 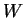 il sottospazio dei vettori
perpendicolari a
il sottospazio dei vettori
perpendicolari a 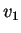 e
e 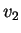 . Si ha necessariamente
. Si ha necessariamente 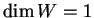 .
.
- Dati in
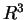 una retta e due punti dire quale delle seguenti affermazioni
è vera:
una retta e due punti dire quale delle seguenti affermazioni
è vera:
1) Esiste sempre un piano che li contiene.
2) Non esiste mai.
3) Se esiste è unico.
4) Ne possono esistere infiniti.
- Siano
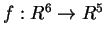 ,
,
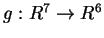 applicazioni lineari. Risulta sempre vero che
applicazioni lineari. Risulta sempre vero che
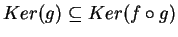 ?
?
Esercizi.
1) Discutere e trovare le soluzioni del seguente sistema al variare del
parametro reale 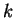 :
:
2) Discutere la diagonalizzabilità della seguente matrice
e trovare, se possibile, una base di autovettori.
3) Sia 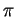 il piano perpendicolare alla retta
il piano perpendicolare alla retta
e passante per il punto
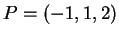 .
.
Sia 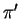 il piano passante per i punti
il piano passante per i punti
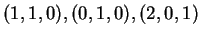 e sia
e sia 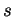 la retta
di intersezione tra
la retta
di intersezione tra 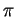 e
e 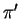 .
.
Sia 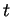 la retta di equazioni
Si studi la posizione reciproca di
la retta di equazioni
Si studi la posizione reciproca di 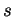 e
e 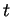 .
.
4) Data la funzione
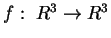 definita da
definita da
scrivere la matrice associata ad 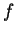 rispetto alla base canonica di
rispetto alla base canonica di 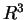 . Determinare
i sottospazi
. Determinare
i sottospazi 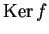 e
e 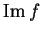 e stabilire se l'applicazione
e stabilire se l'applicazione 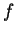 è iniettiva.
Determinare la controimmagine di
è iniettiva.
Determinare la controimmagine di 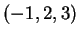 .
.
Soluzione
Domande
- La risposta è no. Infatti il determinante della matrice
è uguale a zero.
- La risposta è no. Infatti
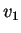 e
e 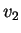 sono proporzionali
il sottospazio dei vettori ortogonali a
sono proporzionali
il sottospazio dei vettori ortogonali a 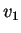 e
e 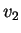 ha dimensione
ha dimensione 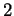 .
.
- Ne possono esistere infiniti.
- La risposta è sì. Infatti se
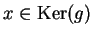 allora
allora
Esercizio 1.
La matrice associata al sistema è la matrice:
Una possibile riduzione a gradino è
Per
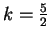 non esistono soluzioni del sistema.
non esistono soluzioni del sistema.
Per 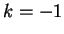 il sistema dato è equivalente al
sistema
il sistema dato è equivalente al
sistema
che ammette infinite soluzioni:
Se
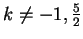 esiste una e una sola soluzione del sistema.
esiste una e una sola soluzione del sistema.
La soluzione è
Esercizio 2.
Il polinomio caratteristico della matrice è :
dumque gli autovalori sono
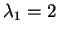 con molteplicità algebrica
con molteplicità algebrica 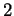 e
e
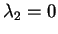 con molteplicità algebrica
con molteplicità algebrica 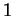 .
.
L'autospazio relativo all'autovalore 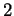 è
che si determina risolvendo il sistema
Risulta allora
Ne deduciamo che la matrice non è diagonalizzabile.
è
che si determina risolvendo il sistema
Risulta allora
Ne deduciamo che la matrice non è diagonalizzabile.
L'autospazio relativo all'autovalore 0 è
e si determina risolvendo il sistema
Risulta allora
Esercizio 3.
Il vettore direttore di 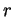 è:
è:
dunque il piano 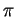 ha equazione cartesiana
Il piano
ha equazione cartesiana
Il piano 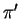 ha equazione cartesiana
pertanto la retta
ha equazione cartesiana
pertanto la retta 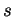 ha equazioni cartesiane
Le equazioni cartesiane di
ha equazioni cartesiane
Le equazioni cartesiane di 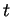 si ottengono eliminando il parametro e si ha:
Per determinare la posizione reciproca delle rette
si ottengono eliminando il parametro e si ha:
Per determinare la posizione reciproca delle rette 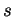 e
e 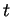 risolviamo il sistema
La matrice completa associata al sistema è:
Riducendo a gradino si ottiene che la matrice completa ha rango
risolviamo il sistema
La matrice completa associata al sistema è:
Riducendo a gradino si ottiene che la matrice completa ha rango 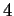 mentre la matrice dei
coefficienti ha rango
mentre la matrice dei
coefficienti ha rango 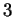 . Pertanto le rette sono sghembe.
. Pertanto le rette sono sghembe.
Esercizio 4.
La matrice della applicazione 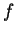 rispetto alla base canonica è:
Il nucleo dell'applicazione si trova come insieme delle soluzioni del sistema omogeneo di
matrice
rispetto alla base canonica è:
Il nucleo dell'applicazione si trova come insieme delle soluzioni del sistema omogeneo di
matrice 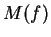 .
.
Riducendo si trova il sistema:
Ne segue che
L'immagine della applicazione 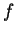 invece è generata dalle colonne linearmente
indipendenti della matrice
invece è generata dalle colonne linearmente
indipendenti della matrice 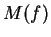 . Risulta:
Infine la controimmagine di
. Risulta:
Infine la controimmagine di 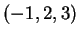 si determina risolvendo il sistema
Le soluzioni sono:
si determina risolvendo il sistema
Le soluzioni sono:




Next: Geometria 2 marzo 1999.
Up: Esercizi
Previous: Geometria 8 febbraio. Tema
Indice
Andreatta Marco
2000-09-18
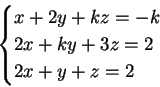
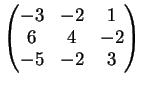
![]() il piano perpendicolare alla retta
il piano perpendicolare alla retta
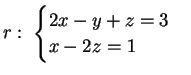
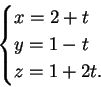
![]() definita da
definita da
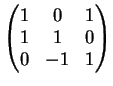
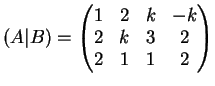
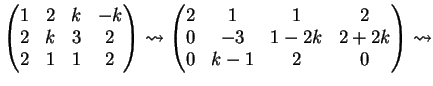
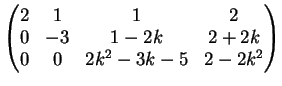
![]() non esistono soluzioni del sistema.
non esistono soluzioni del sistema.
![]() il sistema dato è equivalente al
sistema
il sistema dato è equivalente al
sistema
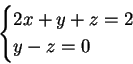
![]() esiste una e una sola soluzione del sistema.
esiste una e una sola soluzione del sistema.
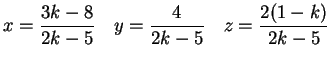
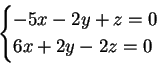
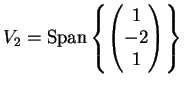
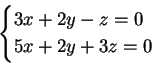
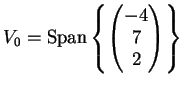
![]() è:
è: