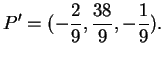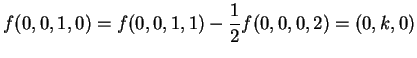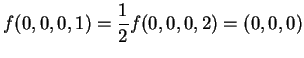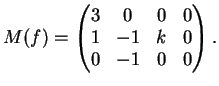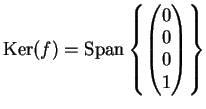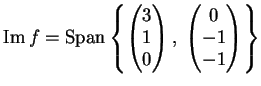Next: Geometria 30 marzo 1999.
Up: Esercizi
Previous: Geometria 2 marzo 1999.
Indice
Rispondere, giustificando brevemente la risposta, ad almeno due delle
prime quattro domande e risolvere il maggior numero degli esercizi seguenti.
Domande.
- Siano
 e
e 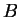 due matrici quadrate . Dimostrare o trovare un
controesempio alla seguente identità:
due matrici quadrate . Dimostrare o trovare un
controesempio alla seguente identità:
- Dire se è vera la seguente affermazione.
Una matrice quadrata di ordine tre il cui polinomio caratteristico è:
è necessariamente diagonalizzabile?
- Siano
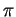 un piano in
un piano in 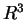 ,
,  e
e  due rette tali che
due rette tali che
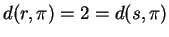 . Quale delle
seguenti affermazioni è vera:
. Quale delle
seguenti affermazioni è vera:
- Le rette
 e
e  sono incidenti.
sono incidenti.
- Le rette
 e
e  sono parallele.
sono parallele.
- Le rette
 e
e  sono sghembe.
sono sghembe.
- Possono verificarsi tutti e tre i casi.
- Siano
 ,
, 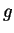 applicazioni lineari da
applicazioni lineari da 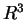 in
in 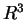 . Risulta sempre vero che
. Risulta sempre vero che
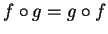 ?
?
È vero se  è l'applicazione nulla?
è l'applicazione nulla?
Esercizi.
1) Discutere e trovare le soluzioni del seguente sistema al variare del
parametro reale 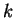 :
:
2) Discutere la diagonalizzabilità della seguente matrice
e trovare, se possibile, una base di autovettori.
3) Siano 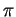 il piano che contiene la retta
il piano che contiene la retta
ed è ortogonale alla retta:
e 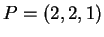 . Si trovi il punto
. Si trovi il punto 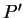 simmetrico di
simmetrico di 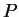 rispetto a
rispetto a 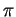 .
.
4) Scrivere la matrice rispetto alle basi canoniche di 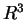 e
e 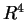 dell'applicazione lineare
dell'applicazione lineare
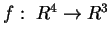 tale che
tale che
dove 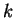 è un parametro reale.
Determinare
i sottospazi
è un parametro reale.
Determinare
i sottospazi 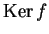 e
e 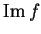 e le loro dimensioni al variare di
e le loro dimensioni al variare di 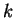 .
.
Soluzione
Domande
- La affermazione è falsa. Si ha per esempio
mentre
- La affermazione è vera. Infatti in questo caso la matrice ha tre
autovalori distinti: 0,
 ,
, 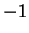 .
.
- Possono verificarsi tutti e tre i casi.
- La risposta è no. Per esempio se
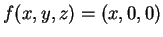 e
e
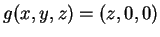 si ha
si ha
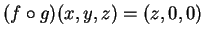 mentre
mentre
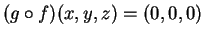 .
.
Se  è l'applicazione nulla allora
è l'applicazione nulla allora
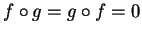 perchè per ogni
applicazione lineare
perchè per ogni
applicazione lineare 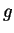 risulta
risulta 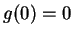 .
.
Esercizio 1.
La matrice dei coefficienti del sistema è la matrice:
Il determinante della matrice  è
pertanto per
è
pertanto per
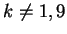 il sistema ammette una unica soluzione.
La soluzione è
Per
il sistema ammette una unica soluzione.
La soluzione è
Per 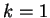 esistono infinite soluzioni :
esistono infinite soluzioni :
Per 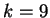 il sistema ammette di nuovo infinite soluzioni :
il sistema ammette di nuovo infinite soluzioni :
Esercizio 2.
Il polinomio caratteristico della matrice è :
dunque gli autovalori sono
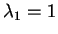 con molteplicità algebrica
con molteplicità algebrica 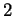 e
e
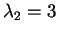 con molteplicità algebrica
con molteplicità algebrica  .
.
L'autospazio relativo all'autovalore  è
che si determina risolvendo il l'equazione
Risulta allora
Ne deduciamo che la matrice è diagonalizzabile.
è
che si determina risolvendo il l'equazione
Risulta allora
Ne deduciamo che la matrice è diagonalizzabile.
L'autospazio relativo all'autovalore 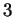 è
e si determina risolvendo il sistema
Risulta allora
è
e si determina risolvendo il sistema
Risulta allora
Esercizio 3.
Il piano 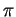 deve essere ortogonale alla retta
deve essere ortogonale alla retta  che ha vettore direttore
che ha vettore direttore 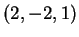 .
Dunque la sua equazione cartesiana sarà della forma
.
Dunque la sua equazione cartesiana sarà della forma
Il piano contiene la retta  e dunque passa per il punto
e dunque passa per il punto 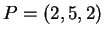 , pertanto deve essere
, pertanto deve essere
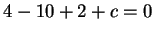 da cui
da cui 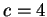 .
Il punto
.
Il punto 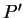 ha coordinate
ha coordinate
Esercizio 4.
Risulta
La matrice della applicazione  rispetto alle basi canoniche è:
Per
rispetto alle basi canoniche è:
Per 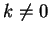 si ha che la dimensione dell'immagine di
si ha che la dimensione dell'immagine di  è uguale al rango di
è uguale al rango di 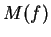 ed
è uguale
ed
è uguale 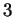 . Il nucleo di
. Il nucleo di  è il sottospazio:
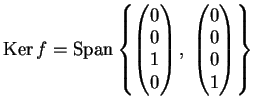
Per
è il sottospazio:
Per 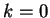 risulta
e
risulta
e




Next: Geometria 30 marzo 1999.
Up: Esercizi
Previous: Geometria 2 marzo 1999.
Indice
Andreatta Marco
2000-09-18
 e
e  sono incidenti.
sono incidenti. e
e  sono parallele.
sono parallele. e
e  sono sghembe.
sono sghembe.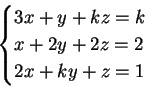
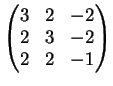
![]() il piano che contiene la retta
il piano che contiene la retta
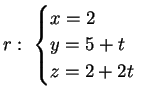
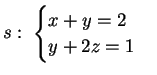
![]() e
e ![]() dell'applicazione lineare
dell'applicazione lineare
![]() tale che
tale che
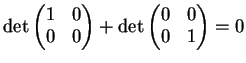
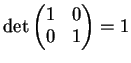
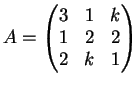
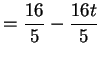
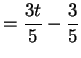
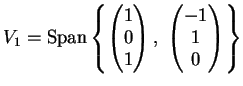
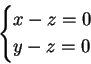

![]() deve essere ortogonale alla retta
deve essere ortogonale alla retta ![]() che ha vettore direttore
che ha vettore direttore ![]() .
Dunque la sua equazione cartesiana sarà della forma
.
Dunque la sua equazione cartesiana sarà della forma