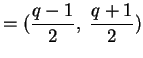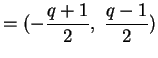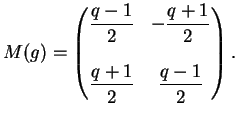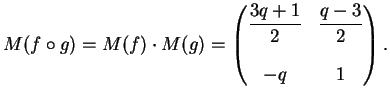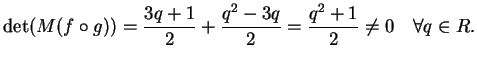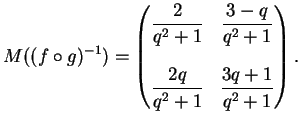Next: Geometria 8 giugno 1999.
Up: Esercizi
Previous: Geometria 30 marzo 1999.
Indice
Rispondere, giustificando brevemente la risposta, ad almeno due delle
prime quattro domande e risolvere il maggior numero degli esercizi seguenti.
Domande.
- Siano
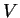 e
e 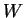 due sottospazi vettoriali di
due sottospazi vettoriali di 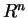 ,
,
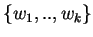 una base di
una base di 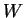 e
e
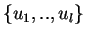 una base di
una base di 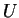 .
E' vero che
.
E' vero che
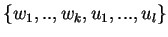 è
una base di
è
una base di 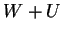 ?
?
- È vera la seguente affermazione: una matrice triangolare è sempre diagonalizzabile?
Dimostrarla o trovare un controesempio.
- Siano
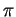 ,
, 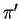 e
e 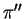 tre piani in
tre piani in 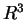 a due a due non paralleli.
Sia
a due a due non paralleli.
Sia  la retta intersezione di
la retta intersezione di 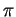 e
e 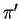 ,
,  la retta intersezione di
la retta intersezione di 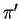 e
e
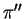 .
Si dica se
.
Si dica se  ed
ed  possono essere sghembe.
possono essere sghembe.
- Siano
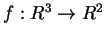 ,
,
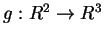 applicazioni lineari con
applicazioni lineari con
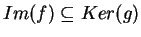 .
Descrivere l'applicazione
.
Descrivere l'applicazione 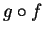 .
.
Esercizi.
1) Discutere e trovare le soluzioni del seguente sistema al variare del
parametro reale 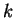 :
:
2) Discutere la diagonalizzabilità della seguente matrice
e trovare, se possibile, una base di autovettori.
3) Sia  la retta passante per
la retta passante per
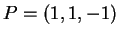 e
e
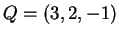 ;
;  la retta perpendicolare
al piano
la retta perpendicolare
al piano
e passante per 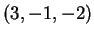 . Si calcoli la distanza di
. Si calcoli la distanza di  ed
ed  .
.
4) Siano
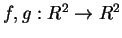 definite da
definite da
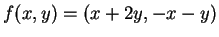 e
e
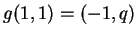 ,
,
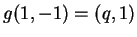 con
con 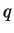 parametro reale.
Determinare i valori di
parametro reale.
Determinare i valori di 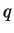 per cui
per cui 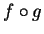 è invertibile e per tali
valori scrivere la matrice dell'inversa rispetto alle basi canoniche.
è invertibile e per tali
valori scrivere la matrice dell'inversa rispetto alle basi canoniche.
Soluzione
Domande
- La risposta è no. Infatti in generale i vettori
sono linearmente dipendenti. Per esempio
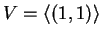 e
e
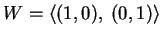 .
.
- La risposta è no. Per esempio la matrice
è triangolare ma non diagonalizzabile.
- La risposta è no. Infatti
 e
e  sono complanari poichè giacciono entrambe sul piano
sono complanari poichè giacciono entrambe sul piano
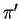 .
.
- La applicazione
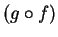 è l'applicazione nulla. Infatti se
è l'applicazione nulla. Infatti se 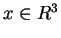 risulta:
poiché, per ipotesi,
risulta:
poiché, per ipotesi,
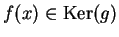 per ogni
per ogni 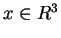 .
.
Esercizio 1.
La matrice associata al sistema è la matrice:
Riduciamo la matrice a gradino usando il mnetodo di Gauss.
Una possibile riduzione è:
Per 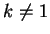 possiamo ridurre ancora e otteniamo la matrice:
Per
possiamo ridurre ancora e otteniamo la matrice:
Per 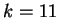 non esistono soluzioni del sistema.
non esistono soluzioni del sistema.
Per 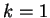 il sistema dato è equivalente al
sistema
che ammette infinite soluzioni:
il sistema dato è equivalente al
sistema
che ammette infinite soluzioni:
Se
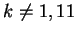 esiste una e una sola soluzione del sistema.
esiste una e una sola soluzione del sistema.
La soluzione è
Esercizio 2.
Il polinomio caratteristico della matrice è :
dunque gli autovalori sono
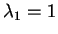 con molteplicità algebrica
con molteplicità algebrica 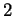 e
e
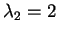 con molteplicità algebrica
con molteplicità algebrica  .
.
L'autospazio relativo all'autovalore  è
è
L'autospazio relativo all'autovalore 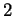 è
è
Concludiamo che la matrice è diagonalizzabile e una base di autovettori è data
Esercizio 3.
La retta  ha equazione parametrica:
mentre la retta
ha equazione parametrica:
mentre la retta  ha equazione parametrica
La direzione di una generica retta incidente
ha equazione parametrica
La direzione di una generica retta incidente  e
e  è
Affinchè questa retta sia ortogonale a
è
Affinchè questa retta sia ortogonale a  deve essere
deve essere
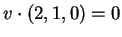 mentre affinchè sia
ortogonale a
mentre affinchè sia
ortogonale a  deve essere
deve essere
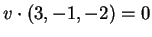 .
Queste due condizioni forniscono il sistema
da cui si ottiene
Il punto di intersezione tra la retta
.
Queste due condizioni forniscono il sistema
da cui si ottiene
Il punto di intersezione tra la retta  e la retta ortogonale ad
e la retta ortogonale ad  e
e  è:
mentre il punto di intersezione tra la retta
è:
mentre il punto di intersezione tra la retta  e la retta ortogonale ad
e la retta ortogonale ad  e
e  è:
La distanza tra le rette
è:
La distanza tra le rette  e
e  è pari alla distanza tra
è pari alla distanza tra 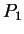 e
e 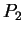 :
Esercizio 4.
:
Esercizio 4.
Scriviamo le matrici di  ,
, 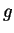 e
e 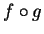 rispetto alla base canonica di
rispetto alla base canonica di 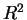 .
.
La matrice della applicazione  è:
Per scrivere la matrice della applicazione
è:
Per scrivere la matrice della applicazione 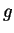 bisogna determinare
bisogna determinare 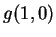 e
e 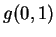 .
.
Ora
pertanto
In definitiva
Risulta allora
Infine la matrice di
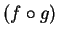 è:
Il determinante della matrice è
Pertanto
è:
Il determinante della matrice è
Pertanto
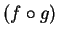 è invertibile per ogni
è invertibile per ogni 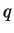 in
in 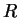 . La matrice
dell'inversa rispetto alla base canonica di
. La matrice
dell'inversa rispetto alla base canonica di 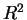 è:
è:




Next: Geometria 8 giugno 1999.
Up: Esercizi
Previous: Geometria 30 marzo 1999.
Indice
Andreatta Marco
2000-09-18
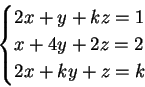
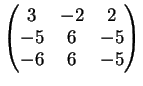
![]() la retta passante per
la retta passante per
![]() e
e
![]() ;
; ![]() la retta perpendicolare
al piano
la retta perpendicolare
al piano
![]() definite da
definite da
![]() e
e
![]() ,
,
![]() con
con ![]() parametro reale.
Determinare i valori di
parametro reale.
Determinare i valori di ![]() per cui
per cui ![]() è invertibile e per tali
valori scrivere la matrice dell'inversa rispetto alle basi canoniche.
è invertibile e per tali
valori scrivere la matrice dell'inversa rispetto alle basi canoniche.
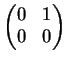
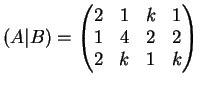
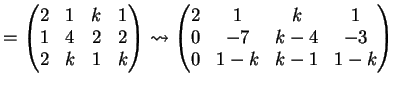
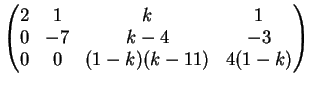
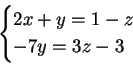
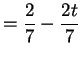
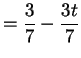
![]() esiste una e una sola soluzione del sistema.
esiste una e una sola soluzione del sistema.
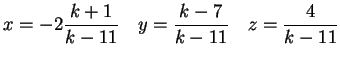
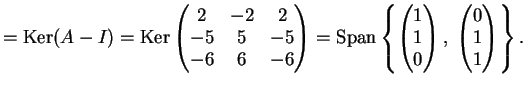
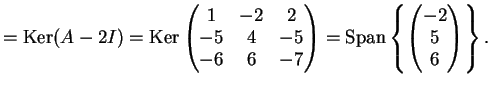
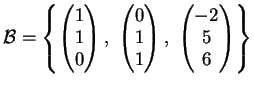
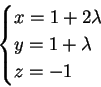
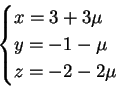
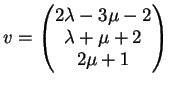
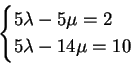
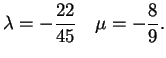
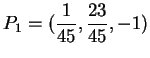
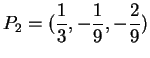
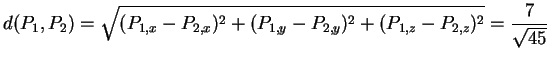
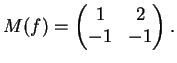
![$\displaystyle = \frac{1}{2} \left [ (1,1)+(1,-1) \right ]$](img1364.gif)
![$\displaystyle = \frac{1}{2} \left [ (1,1)-(1,-1) \right ],$](img1366.gif)
![$\displaystyle = \frac{1}{2} \left [ g(1,1)+ g(1,-1) \right ]= \frac{1}{2} \left [ (-1,q)+(q,1) \right ]$](img1368.gif)
![$\displaystyle = \frac{1}{2} \left [ g(1,1)- g(1,-1) \right ]= \frac{1}{2} \left [ (-1,q)-(q,1) \right ],$](img1370.gif)