



Next: Applicazioni lineari
Up: Esercizi
Previous: Sistemi lineari
Indice
Esercizio 26
Determinare se i seguenti sottoinsiemi sono sottospazi di

:
Dimostrazione.
L'insieme
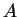
è costituito dai vettori
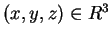
tali che
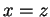
.
Poichè
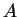
è l'insieme delle soluzioni di una equazione lineare omogenea,
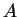
è un sottospazio di

.
Verifichiamo direttamente che
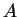
è un sottospazio di

.
Abbiamo:
La somma di due vettori di
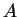
è ancora un vettore in
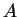
, infatti:
Il prodotto di un vettore di
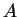
per uno scalare è ancora un vettore di
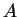
,
infatti:
Il sottoinsieme
è l'insieme delle soluzioni di una equazione lineare non omogenea e pertanto
non è un sottospazio. di

. È facile anche verificare che, per esempio,
il vettore nullo non appartiene a
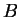
.
Il sottoinsieme 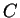 di
di  è costituito dai vettori della forma
è costituito dai vettori della forma
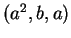 al variare di
al variare di 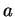 e
e 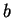 in
in 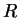 . Dati due vettori di
. Dati due vettori di 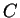 ,
,
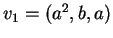 e
e
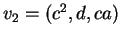 , il vettore somma
, il vettore somma
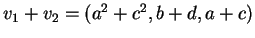 in generale non
è un elemento di
in generale non
è un elemento di 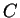 . Infatti
. Infatti
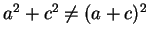 se
se 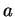 e
e 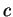 sono
entrambi non nulli. Ne segue che
sono
entrambi non nulli. Ne segue che 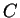 non è chiuso rispetto alla somma e dunque
non è un sottospazio.
non è chiuso rispetto alla somma e dunque
non è un sottospazio.
Il sottoinsieme 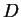 è costituito dai vettori di
è costituito dai vettori di  che sono soluzioni del sistema lineare
omogeneo
che sono soluzioni del sistema lineare
omogeneo
pertanto è un sottospazio di

. I suoi elementi sono i vettori della forma
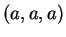
al
variare di
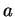
in
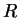
.
Il sottoinsieme 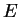 è costituito dal solo vettore nullo, infatti l'equazione
è costituito dal solo vettore nullo, infatti l'equazione
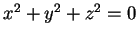 è soddisfatta solo per
è soddisfatta solo per 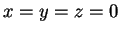 . Ne segue che
. Ne segue che 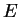 è il sottospazio banale di
è il sottospazio banale di  .
.
Infine il sottoinsieme 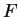 è costituito dai vettori
è costituito dai vettori 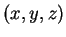 di
di  tali che
tali che
ovvero dai vettori di

tali che
Un generico vettore di
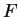
si scrive allora come
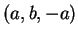
per certi
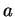
e
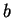
in
.
Si verifica
facilmente che
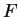
è chiuso rispetto alla somma e al prodotto per uno scalare.
Infatti:
e

Esercizio 27
Sia

il sottospazio di

generato dai vettori
Scrivere

come spazio delle soluzioni di un sistema lineare omogeneo.
Dimostrazione.
Gli elementi del sottospazio

sono i vettori
al variare di
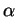
e
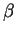
in
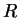
.
Abbiamo allora:
Al variare di
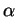
e
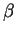
in
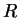
,
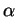
e
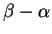
descrivono tutto
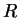
,
pertanto:

Esercizio 28
Dire quali dei seguenti sottoinsiemi di

sono formati da vettori
linearmente indipendenti:
Dimostrazione.
L'insieme
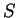
è costituito dai vettori
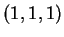
e
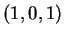
che sono linearmente indipendenti.
Infatti due vettori sono linearmente dipendenti se e solo se sono proporzionali. È facile
verificare che in questo caso non esiste alcun
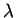
in
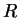
tale che
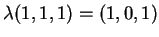
.
I tre vettori in 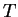 non sono linearmente indipendenti perchè il terzo è somma dei primi due.
I vettori
non sono linearmente indipendenti perchè il terzo è somma dei primi due.
I vettori 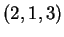 e
e 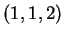 sono invece indipendenti poichè non esiste alcun
sono invece indipendenti poichè non esiste alcun
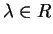 tale che
tale che
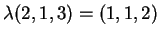 .
.
L'insieme 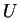 è costituito dai vettori
è costituito dai vettori 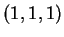 ,
, 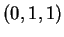 e
e 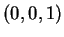 . Per verificare se si
tratta di vettori indipendenti calcoliamo il determinante della matrice formata dai tre vettori:
. Per verificare se si
tratta di vettori indipendenti calcoliamo il determinante della matrice formata dai tre vettori:
Risulta
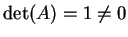
pertanto i vettori di
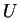
sono linearmente indipendenti.
Infine il sottoinsieme  è un sottospazio di
è un sottospazio di  e pertanto non è costituito da vettori
linearmente indipendenti. Per esempio perchè contiene il vettore nullo, oppure perchè
dato un vettore
ne contiene ogni multiplo.
e pertanto non è costituito da vettori
linearmente indipendenti. Per esempio perchè contiene il vettore nullo, oppure perchè
dato un vettore
ne contiene ogni multiplo.

Esercizio 29
Provare che l'insieme
è un sistema di generatori di

. Estrarre una base di

dagli
elementi di
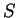
.
Dimostrazione.
Proviamo che l'insieme
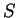
genera

. Si tratta di far vedere che ogni vettore di

si può
scrivere come combinazione lineare degli elementi di
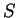
. Per ogni
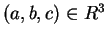
vogliamo
trovare
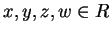
tali che
Otteniamo un sistema lineare la cui matrice completa è :
Una possibile riduzione per righe è :
Se ne deduce che il sistema ammette sempre (infinite) soluzioni e dunque
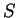
genera

.
I vettori di
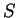
sono in numero maggiore della dimensione di

quindi non possono essere
tutti
linearmente indipendenti. Infatti risulta:
D'altra parte i tre vettori
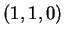
,
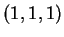
e
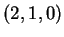
sono indipendenti e pertanto
costituiscono una base di

.

Esercizio 30
Determinare una base del sottospazio di

formato dalle soluzioni
dell'equazione
Dimostrazione.
Le soluzioni dell'equazione sono tutti e soli i vettori di

della forma
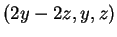
al
variare di
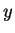
e
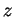
in
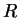
. Ora:
sicchè l'insieme
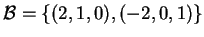
genera il sottospazio. Poichè i vettori
di
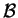
sono
linearmente indipendenti l'insieme
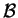
è una base del sottospazio.

Dimostrazione.
Il sottoinsieme
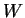
è costituito dalle soluzioni dell'equazione
pertanto è un sottospazio
di

. Inoltre possiamo scrivere:
Un generico vettore di
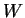
è combinazione lineare dei vettori
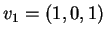
e
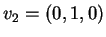
poichè:
I vettori
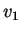
e
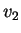
sono linearmente indipendenti così l'insieme
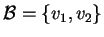
è una base di
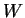
e risulta
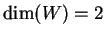
.
Infine il vettore 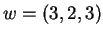 appartiene a
appartiene a 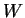 perchè la prima e la terza componente coincidono.
Le sue coordinate rispetto alla base ordinata
perchè la prima e la terza componente coincidono.
Le sue coordinate rispetto alla base ordinata
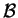 sono rispettivamente
sono rispettivamente 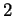 e
e 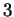 :
:

Esercizio 32
Sia
un sottoinsieme di vettori linermente indipendenti in uno spazio vettoriale
reale

.
Provare che anche
è un sottoinsieme di vettori linearmente indipendenti.
Dimostrazione.
Per provare che i vettori di
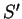
sono linearmente indipendenti supponiamo di avere una combinazione
lineare uguale al vettore nullo e proviamo che allora i coefficienti della combinazione devono essere
tutti nulli.
Supponiamo dunque di avere:
Questo implica che sia:
L'ultima equazione è una combinazione lineare dei vettori di
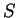
uguale al vettore nullo.
Poichè
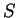
è un sottoinsieme di vettori linearmente indipendenti, i coefficienti della
combinazione devono
essere tutti nulli, ovvero deve essere:
e dunque
Abbiamo così mostrato che
ovvero che l'unica combinazione lineare dei vettori di
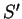
uguale al vettore nullo è quella i cui
coefficienti siano tutti nulli.

Esercizio 33
Determinare i valori del parametro reale
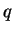
per i quali i tre vettori di
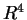
:
sono linearmente dipendenti. Per tali valori esprimere uno dei tre vettori come
combinazione lineare degli altri due.
Dimostrazione.
I vettori
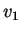
,
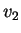
e
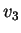
sono linearmente dipendenti se e solo se la matrice
non ha rango massimo. Per determinare il rango di
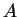
riduciamola a gradino.
Una possibile riduzione è:
La matrice
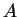
ha rango
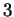
per
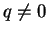
e rango
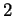
per
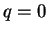
. Per
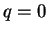
i vettori
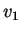
,
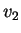
e
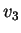
sono allora linearmente dipendenti. Inoltre
Si vede facilmente che
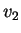
è combinazione lineare di
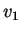
e
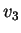
, infatti:

Esercizio 34
Determinare la dimensione e una base dei seguenti sottospazi di

:
Dimostrazione.
Il sottospazio
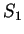
è generato dai vettori
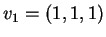
e
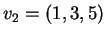
, che sono
linearmente indipendenti. Ne segue che
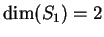
e una base di
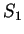
è
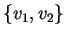
.
Il sottospazio  è generato dai vettori
è generato dai vettori
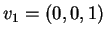 ,
,
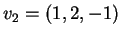 e
e
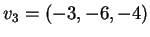 , che non sono indipendenti. Infatti:
, che non sono indipendenti. Infatti:
D'altra parte
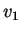
e
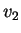
sono linearmente indipendenti pertanto
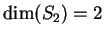
e una base
di

è
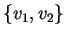
.
Infine 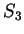 è generato dai vettori
è generato dai vettori
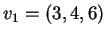 ,
,
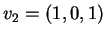 e
e
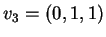 . I tre
vettori sono linearmente indipendenti perchè
. I tre
vettori sono linearmente indipendenti perchè
Allora la dimensione di
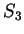
è
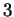
e una base di
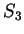
è
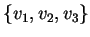
.

Esercizio 35
Dati i vettori di
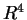
:
sia

il sottospazio
Determinare una base di

.
Dimostrazione.
La dimensione di

è uguale al rango della matrice
Una possibile riduzione per righe della matrice
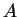
è la seguente:
La dimensione di

è uguale a
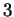
. Inoltre i vettori
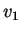
,
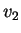
e
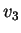
costituiscono
una base per

. Per dimostrare l'ultima affermazione basta osservare che, dalla riduzione
fatta sopra, segue che la matrice
ha rango
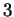
. Un'altra scelta possibile per una base di

è
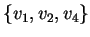
.

Esercizio 36
Sia
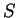
il sottoinsieme di

Determinare i valori del parametro reale
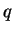
per i quali
Dimostrazione.
Si tratta di trovare i valori del parametro
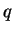
per i quali il sistema:
ha soluzione.
Il sistema si riscrive:
ed ha soluzione se e solo se
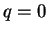
.

Dimostrazione.
Per determinare la dimensione di

verifichiamo se i vettori
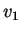
,
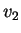
e
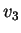
sono
linearmente indipendenti.
Si tratta allora di determinare le soluzioni del sistema omogeneo
La matrice dei coefficienti del sistema è:
che, ridotta a gradino, diventa:
Per
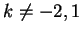
il sistema ammette solo la soluzione banale dunque i vettori
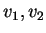
e
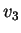
sono linearmente indipendenti. Questo significa che per
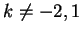
la dimensione di

è
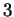
( ovvero
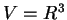
) e una sua base è
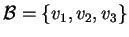
.
Se 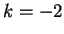 o
o 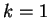 invece i vettori
invece i vettori 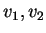 e
e 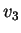 sono linearmente dipendenti dunque la
dimensione di
sono linearmente dipendenti dunque la
dimensione di  è minore di
è minore di 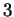 .
.
Per 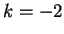 abbiamo:
abbiamo:
I vettori
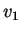
e
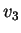
sono linearmente indipendenti perchè non sono proporzionali sicchè la
dimensione di

è
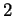
e una sua base è, per esempio,
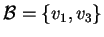
.
Un'altra scelta possibile per una base di

è l'insieme
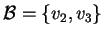
mentre i
vettori
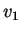
e
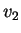
non costituiscono una base di

perchè sono dipendenti (proporzionali).
Infine per 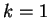 abbiamo
abbiamo
Di nuovo i vettori
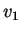
e
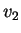
sono linearmente indipendenti, la dimensione di

è
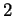
e
una sua base è
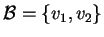
.
Determiniamo ora i valori del parametro reale 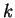 per i quali il vettore
per i quali il vettore 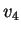 è combinazione
lineare dei primi tre.
è combinazione
lineare dei primi tre.
Per
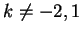 abbiamo visto che
abbiamo visto che  coincide con
coincide con  e
e
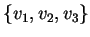 è una base
di
è una base
di  . Allora per
. Allora per
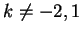 il vettore
il vettore 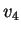 è sicuramente combinazione lineare di
è sicuramente combinazione lineare di
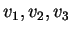 . Per determinare i coefficienti della combinazione lineare risolviamo il sistema
. Per determinare i coefficienti della combinazione lineare risolviamo il sistema
La matrice completa associata al sistema è :
che, ridotta a gradino, diventa:
Per
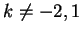
abbiamo una unica soluzione
Per
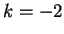
consideriamo la base
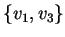
di

. Di nuovo dobbiamo risolvere il sistema
La matrice del sistema è:
che, ridotta a gradino diventa
Segue che il sistema non ha soluzioni ovvero
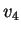
non è combinazione degli elementi di una
base di

ovvero
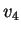
non appartiene a

.
Per 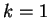 consideriamo la base
consideriamo la base
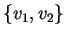 e risolviamo il sistema
e risolviamo il sistema
La matrice del sistema è:
che, ridotta a gradino diventa
Come nel caso precedente si conclude che
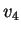
non appartiene a

.

Esercizio 38
Determinare i valori del parametro
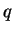
per cui la somma dei sottospazi di

:
è una somma diretta.
Dimostrazione.
La somma dei sottospazi
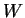
e
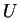
è diretta se e solo se
Supponiamo esista un vettore
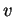
in
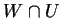
, sarà allora:
per certi
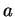
,
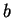
e
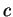
in
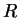
.
Allora deve anche essere:
Se
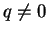
troviamo che
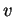
deve essere il vettore nullo, mentre se
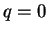
ogni vettore
della forma
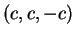
è nell'intersezione.
Riassumendo la somma di 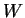 e
e 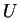 è diretta se e solo se
è diretta se e solo se 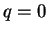 .
.

Esercizio 39
Determinare una base di

rispetto alla quale il vettore
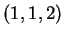
ha
componenti
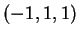
.
Dimostrazione.
Sia
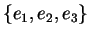
la base canonica di

, così
Poniamo
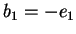
,
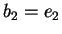
e
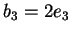
. È facile verificare che
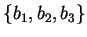
è
ancora una base di

. Inoltre

Esercizio 40
Provare che se
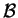
,
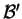
sono basi di due sottospazi
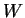
e
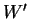
di
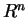
tali che
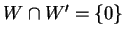
, allora
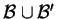
è base
di
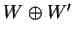
.
Dimostrazione.
Indichiamo con
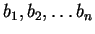
gli elementi di
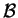
e con
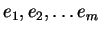
gli elementi di
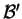
.
Proviamo che
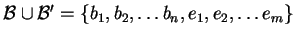 genera
genera
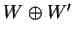 .
.
Sia 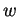 un vettore di
un vettore di
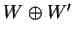 , allora
, allora 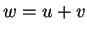 con
con 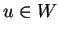 e
e 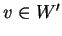 . Poichè
. Poichè
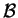 è una base di
è una base di 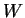 , sarà :
, sarà :
e, poichè
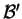
è una base di
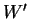
, sarà anche:
Ne segue che :
sicchè
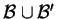
genera
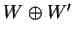
.
Ora proviamo che i vettori di
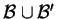 sono linearmente indipendenti. Supponiamo
di avere una loro combinazione lineare uguale al vettore nullo:
sono linearmente indipendenti. Supponiamo
di avere una loro combinazione lineare uguale al vettore nullo:
Allora
dunque il vettore
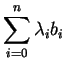
appartiene a sia a
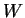
che a
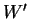
. Siccome la
somma è diretta deve essere
D'altra parte
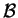
è una base di
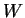
, dunque
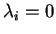
, per
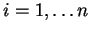
.
Ragionando nello stesso modo per il vettore
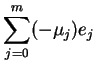
, si
trova che
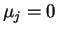
per
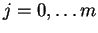
.

Esercizio 41
Date le matrici
provare che l'insieme
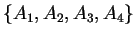
è un insieme linearmente
indipendente nello spazio delle matrici
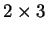
a coefficienti reali.
Dimostrazione.
Nello spazio delle matrici
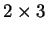
a coefficienti reali il vettore nullo è la matrice
nulla. Per provare che l'insieme
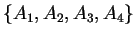
è un insieme linearmente
indipendente, supponiamo di avere una combinazione lineare dei suoi elementi uguale
alla
matrice nulla:
Deve allora essere
La matrice associata al sistema è:
che, ridotta a gradino, diventa:
Il sistema ammette una e una sola soluzione, necessariamente banale:

Esercizio 42
Provare che le seguenti matrici
sono una base del sottospazio vettoriale delle matrici
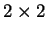
a
coefficienti reali formato dalle matrici simmetriche.
Dimostrazione.
Una matrice
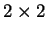
simmetrica è della forma:
Le matrici
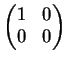
,
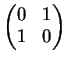
e
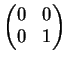
generano il sottospazio delle matrici simmetriche perchè:
Inoltre sono linearmente indipendenti perchè l'uguaglianza:
implica
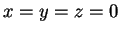
.





Next: Applicazioni lineari
Up: Esercizi
Previous: Sistemi lineari
Indice
Andreatta Marco
2000-09-18
![]() di
di ![]() è costituito dai vettori della forma
è costituito dai vettori della forma
![]() al variare di
al variare di ![]() e
e ![]() in
in ![]() . Dati due vettori di
. Dati due vettori di ![]() ,
,
![]() e
e
![]() , il vettore somma
, il vettore somma
![]() in generale non
è un elemento di
in generale non
è un elemento di ![]() . Infatti
. Infatti
![]() se
se ![]() e
e ![]() sono
entrambi non nulli. Ne segue che
sono
entrambi non nulli. Ne segue che ![]() non è chiuso rispetto alla somma e dunque
non è un sottospazio.
non è chiuso rispetto alla somma e dunque
non è un sottospazio.
![]() è costituito dai vettori di
è costituito dai vettori di ![]() che sono soluzioni del sistema lineare
omogeneo
che sono soluzioni del sistema lineare
omogeneo
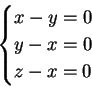
![]() è costituito dal solo vettore nullo, infatti l'equazione
è costituito dal solo vettore nullo, infatti l'equazione
![]() è soddisfatta solo per
è soddisfatta solo per ![]() . Ne segue che
. Ne segue che ![]() è il sottospazio banale di
è il sottospazio banale di ![]() .
.
![]() è costituito dai vettori
è costituito dai vettori ![]() di
di ![]() tali che
tali che
![]() non sono linearmente indipendenti perchè il terzo è somma dei primi due.
I vettori
non sono linearmente indipendenti perchè il terzo è somma dei primi due.
I vettori ![]() e
e ![]() sono invece indipendenti poichè non esiste alcun
sono invece indipendenti poichè non esiste alcun
![]() tale che
tale che
![]() .
.
![]() è costituito dai vettori
è costituito dai vettori ![]() ,
, ![]() e
e ![]() . Per verificare se si
tratta di vettori indipendenti calcoliamo il determinante della matrice formata dai tre vettori:
. Per verificare se si
tratta di vettori indipendenti calcoliamo il determinante della matrice formata dai tre vettori:
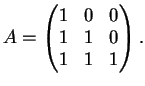
![]() è un sottospazio di
è un sottospazio di ![]() e pertanto non è costituito da vettori
linearmente indipendenti. Per esempio perchè contiene il vettore nullo, oppure perchè
dato un vettore
ne contiene ogni multiplo.
e pertanto non è costituito da vettori
linearmente indipendenti. Per esempio perchè contiene il vettore nullo, oppure perchè
dato un vettore
ne contiene ogni multiplo.
![]()
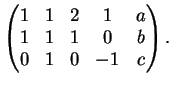
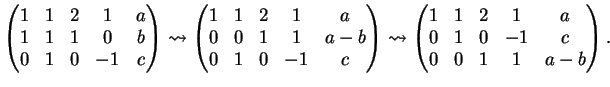
![]() appartiene a
appartiene a ![]() perchè la prima e la terza componente coincidono.
Le sue coordinate rispetto alla base ordinata
perchè la prima e la terza componente coincidono.
Le sue coordinate rispetto alla base ordinata
![]() sono rispettivamente
sono rispettivamente ![]() e
e ![]() :
:
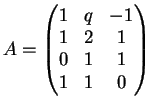
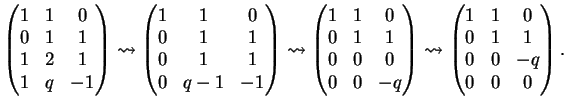
![]() è generato dai vettori
è generato dai vettori
![]() ,
,
![]() e
e
![]() , che non sono indipendenti. Infatti:
, che non sono indipendenti. Infatti:
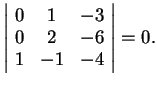
![]() è generato dai vettori
è generato dai vettori
![]() ,
,
![]() e
e
![]() . I tre
vettori sono linearmente indipendenti perchè
. I tre
vettori sono linearmente indipendenti perchè
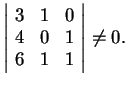
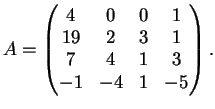
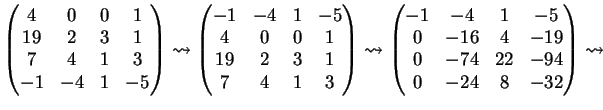
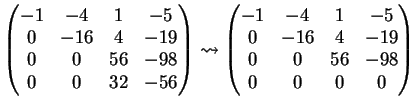
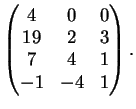
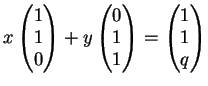

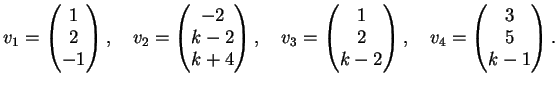
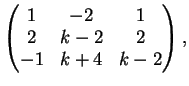
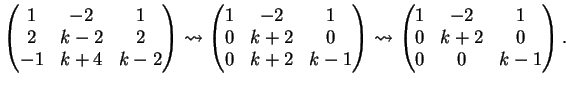
![]() o
o ![]() invece i vettori
invece i vettori ![]() e
e ![]() sono linearmente dipendenti dunque la
dimensione di
sono linearmente dipendenti dunque la
dimensione di ![]() è minore di
è minore di ![]() .
.
![]() abbiamo:
abbiamo:
![]() abbiamo
abbiamo
![]() per i quali il vettore
per i quali il vettore ![]() è combinazione
lineare dei primi tre.
è combinazione
lineare dei primi tre.
![]() abbiamo visto che
abbiamo visto che ![]() coincide con
coincide con ![]() e
e
![]() è una base
di
è una base
di ![]() . Allora per
. Allora per
![]() il vettore
il vettore ![]() è sicuramente combinazione lineare di
è sicuramente combinazione lineare di
![]() . Per determinare i coefficienti della combinazione lineare risolviamo il sistema
. Per determinare i coefficienti della combinazione lineare risolviamo il sistema
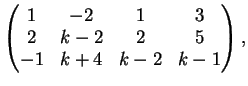
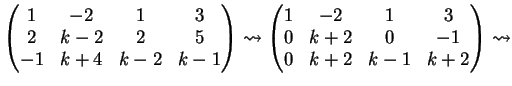
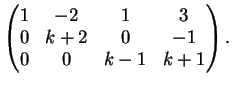
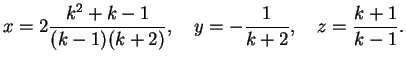
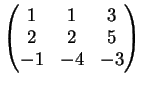
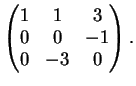
![]() consideriamo la base
consideriamo la base
![]() e risolviamo il sistema
e risolviamo il sistema
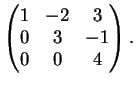

![]() e
e ![]() è diretta se e solo se
è diretta se e solo se ![]() .
.
![]()
![]() genera
genera
![]() .
.
![]() un vettore di
un vettore di
![]() , allora
, allora ![]() con
con ![]() e
e ![]() . Poichè
. Poichè
![]() è una base di
è una base di ![]() , sarà :
, sarà :
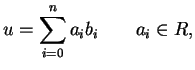
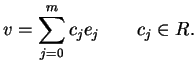
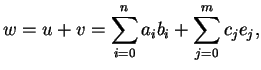
![]() sono linearmente indipendenti. Supponiamo
di avere una loro combinazione lineare uguale al vettore nullo:
sono linearmente indipendenti. Supponiamo
di avere una loro combinazione lineare uguale al vettore nullo:
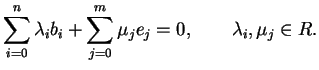
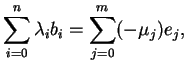
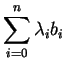 appartiene a sia a
appartiene a sia a 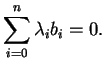
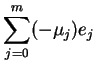 , si
trova che
, si
trova che 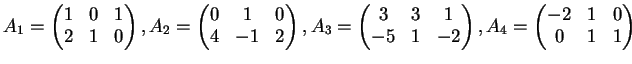
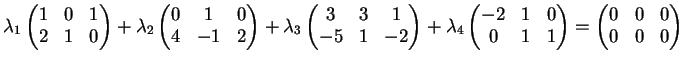
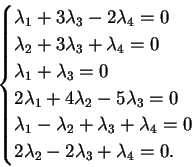
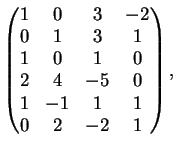
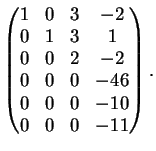
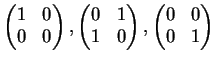
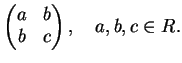
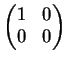 ,
,
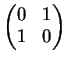 e
e
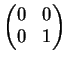 generano il sottospazio delle matrici simmetriche perchè:
generano il sottospazio delle matrici simmetriche perchè:
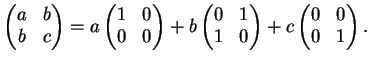
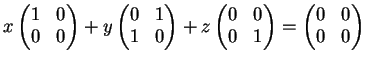
![]()