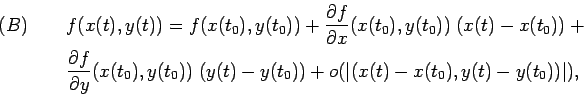TEOREMA (Del differenziale totale): Sia
TEOREMA (Del differenziale totale): Sia
![]() una funzione derivabile parzialmente in un intorno del punto
una funzione derivabile parzialmente in un intorno del punto
![]() (cioè in un
rettangolo che contiene
(cioè in un
rettangolo che contiene ![]() al suo interno). Se le
derivate parziali
al suo interno). Se le
derivate parziali
![]() ,
,
![]() sono entrambe continue nel punto
sono entrambe continue nel punto ![]() ,
allora la funzione
,
allora la funzione ![]() è differenziabile nel punto
è differenziabile nel punto ![]() .
.
ESEMPIO: Riprendiamo la funzione
![]() , di cui
avevamo verificato ``a mano'' la differenziabilità. Si ha
, di cui
avevamo verificato ``a mano'' la differenziabilità. Si ha
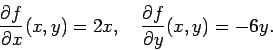
In maniera analoga, un qualunque polinomio di due variabili è ovunque differenziabile, perché le sue derivate parziali sono ancora polinomi e sappiamo che i polinomi sono funzioni continue... Utilizzando il teorema del differenziale totale, si può così mostrare facilmente che un gran numero di funzioni elementari sono differenziabili.
DIMOSTRAZIONE del Teorema del Differenziale Totale: Sia ![]() un punto sufficientemente vicino a
un punto sufficientemente vicino a ![]() , in modo che tutto il rettangolo di
vertici
, in modo che tutto il rettangolo di
vertici ![]() ,
, ![]() ,
, ![]() e
e ![]() sia contenuto nell'insieme
in cui esistono le derivate parziali di
sia contenuto nell'insieme
in cui esistono le derivate parziali di ![]() .
.
Per mostrare che ![]() è differenziabile in
è differenziabile in ![]() , dobbiamo far vedere
che quando
, dobbiamo far vedere
che quando
![]() il seguente rapporto tende a
il seguente rapporto tende a ![]() :
:
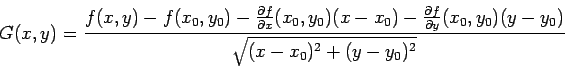
Il teorema di Lagrange per funzioni di una variabile mi assicura che esistono
dei punti ![]() (con
(con ![]() compreso tra
compreso tra ![]() ed
ed ![]() ) ed
) ed ![]() (con
(con ![]() compreso tra
compreso tra ![]() ed
ed ![]() ) tali che
) tali che
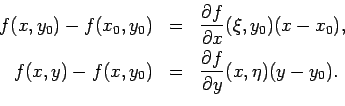
Nel rapporto ![]() , aggiungiamo e togliamo la quantità
, aggiungiamo e togliamo la quantità ![]() a
numeratore, ed applichiamo le due relazioni appena trovate. Possiamo così
scrivere
a
numeratore, ed applichiamo le due relazioni appena trovate. Possiamo così
scrivere
![\begin{eqnarray*}
G(x,y)&=&\frac{x-x_0}{\sqrt{(x-x_0)^2+(y-y_0)^2}}\left[\frac{...
...ial y}
(x,\eta)-\frac{\partial f}{\partial y}(x_0,y_0)\right].
\end{eqnarray*}](img304.gif)
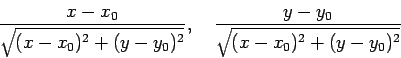
OSSERVAZIONE: Il teorema del differenziale totale
ci fornisce solo una condizione
sufficiente di differenziabilità: una funzione può benissimo
essere differenziabile anche se non sono soddisfatte le ipotesi.
Ad esempio, la funzione

Esattamente come accadeva in una variabile, l'analisi delle derivate
parziali è un metodo potentissimo per cercare i punti di
massimo e minimo relativo per una funzione differenziabile di due variabili.
Una prima semplicissima osservazione ci assicura che in un punto di massimo o
minimo relativo il piano tangente deve essere orizzontale:
OSSERVAZIONE: Se ![]() è un punto di massimo o minimo
relativo per la funzione differenziabile
è un punto di massimo o minimo
relativo per la funzione differenziabile ![]() , allora
, allora
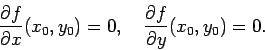
I punti in cui il piano tangente è orizzontale si chiamano punti
critici.
Evidentemente, questi non sono tutti punti
di massimo o minimo relativo: ci possono essere per esempio
punti di sella (punti
corrispondenti a un ``passo di montagna'', se interpretiamo il grafico
della funzione come rappresentazione grafica di un territorio montuoso...).
Così come facevamo in una variabile, ci piacerebbe classificare i punti
critici in base al segno della derivata seconda. Un piccolo problemino è
dato però dal fatto che in un punto ![]() di possibili derivate seconde ce ne sono ben
quattro:
di possibili derivate seconde ce ne sono ben
quattro:
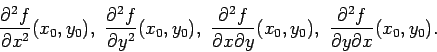
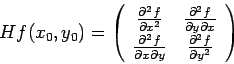
Per nostra fortuna, se la funzione ![]() è abbastanza buona le due
derivate parziali miste sono uguali e la
matrice hessiana è una matrice simmetrica: è il contenuto del seguente
è abbastanza buona le due
derivate parziali miste sono uguali e la
matrice hessiana è una matrice simmetrica: è il contenuto del seguente
TEOREMA (di Schwartz): Se ![]() possiede entrambe le derivate
seconde miste
possiede entrambe le derivate
seconde miste
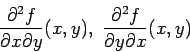
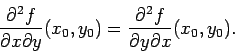
Omettiamo la dimostrazione del teorema di Schwartz (che comunque non è
molto più difficile di quella del teorema del differenziale totale).
Osserviamo però che il teorema può essere falso se non valgono le
ipotesi: esistono esempi di funzioni che hanno le derivate seconde miste
diverse!
Purtroppo questa non è una questione di lana caprina: la simmetria della matrice hessiana sarà una proprietà molto importante nel nostro studio dei punti critici10.
Come per le funzioni di una variabile, lo studio dei punti critici mediante le derivate seconde è strettamente legato ad una formula di Taylor di ordine 2 (con resto di Peano). Per poterla dimostrare, ci serve una semplice regola di derivazione delle funzioni composte che è molto interessante anche per se stessa:
PROPOSIZIONE (Regola di derivazione delle funzioni composte):
Sia ![]() una funzione ovunque differenziabile, e siano
una funzione ovunque differenziabile, e siano ![]() ,
, ![]() due
funzioni derivabili di una variabile. Allora la funzione composta
due
funzioni derivabili di una variabile. Allora la funzione composta
![]() è derivabile, e si ha
è derivabile, e si ha
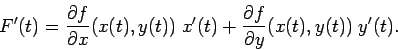
DIM: Per dimostrare che ![]() è derivabile in
è derivabile in ![]() e che vale
la nostra espressione per la derivata, è sufficiente verificare che vale
la formula di Taylor del primo ordine:
e che vale
la nostra espressione per la derivata, è sufficiente verificare che vale
la formula di Taylor del primo ordine:
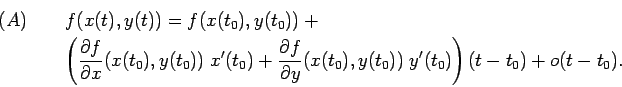
A questo scopo, notiamo che la differenziabilità di ![]() implica
implica