Il problema di Plateau: lamine saponate e superfici minime

Poster realizzato da:	Sisto Baldo
	Dipartimento di Matematica
	Università della Basilicata.

Prendiamo un contorno chiuso fatto di filo metallico, immergiamolo nell'acqua saponata ed estraiamolo delicatamente. Scopriremo che sul filo si appoggia una pellicola di sapone, che a seconda della forma del contorno assume forme diverse e spesso bellissime.

Saper prevedere la come si dispone la pellicola saponata costituisce un problema matematico noto come Problema di Plateau, dal nome del fisico belga J.A.F. Plateau (1801-1883).

La lamina di sapone si dispone, in effetti, a formare una superficie la cui area sia la minima possibile tra quelle aventi quel dato contorno. Questo avviene perché la tensione superficiale della lamina saponata tende a ridurne il più possibile l'estensione. Il fenomeno è ben visibile nella figura, in cui si è usato un contorno costituito in parte da fili flessibili: i fili vengono flessi marcatamente verso l'interno dalle forze di tensione che tentano di ridurre la superficie della lamina.

Se il contorno è costituito da due cerchi paralleli sufficientemente vicini, la superficie che osserviamo non è il cilindro, come forse potremmo pensare. Osserviamo invece una superficie di rotazione chiamata catenoide. Infatti, se è vero che nella catenoide le curve verticali che costituiscono le generatrici della superficie sono più lunghe dei segmenti di retta che abbiamo nel cilindro, la nostra superficie è però più stretta al centro, e questo a conti fatti ci fa risparmiare area! Questo è un fatto matematico che i film di sapone conoscono alla perfezione.

Del resto, i film di sapone sono anche perfettamente in grado di costruire una scala a chiocciola, senza bisogno dei disegni di un architetto: la superficie a sinistra si chiama elicoide.

Se utilizziamo contorni più complicati, come ad esempio lo scheletro di un cubo (a destra), si formano più lamine che si incontrano soddisfacendo ad alcune condizioni geometriche: ad esempio, quando tre lamine si incontrano, formano sempre angoli di 120${}^\circ$. Anche la superficie a sella triangolare (a destra, sotto i cubi) è interessante: gli ingegneri la usano come modulo per la costruzione di alcuni tipi di tensostruttura (ad esempio, i tendoni all'aperto di certi ristoranti).

La disposizione delle lamine saponate non dipende solo dalla forma del contorno, ma anche dalle sue dimensioni: nella figura sopra, vediamo che a prismi di altezza diversa (a base quadrata o triangolare) corrispondono disposizioni completamente diverse delle lamine saponate. Usando prismi ad altezza regolabile, è anche possibile vedere il salto tra le due diverse configurazioni. Accanto ai prismi, una sorridente Marta Cazzanelli del Laboratorio LRM${}^3$D${}^2$ del Dipartimento di Matematica dell'Università di Trento.

Se su una lamina saponata piana appoggiamo un cappio di filo da cucire, e facciamo scoppiare la parte di superficie all'interno del cappio, si forma un buco perfettamente circolare. La lamina saponata, infatti, ha cercato di massimizzare l'area del buco, ed ha trovato la soluzione del problema isoperimetrico nel piano: tra tutte le figure piane di assegnato perimetro, il cerchio è quella di area massima.

Continuamo la nostra carrellata con alcune immagini virtuali di superfici minime. Ad esempio, sopra e sotto questa pagina vediamo un elicoide e una catenoide, superfici di cui abbiamo già visto la realizzazione fisica mediante lamine saponate.

Grazie al calcolatore, possiamo però vedere anche superfici minime che non sono realizzabili con film di sapone. In matematica, per superficie minima si intende infatti una superficie che localmente minimizza l'area: per questo motivo, non tutte le superfici minime sono film di sapone!

Sopra questa pagina, vediamo la superficie a sella di Enneper, di equazioni parametriche

$$\left\{ \begin{array}{l} x(u,v)=u-\frac{1}{3} u^3+uv^2\\ y(u... ...v-u^2v+\frac{1}{3} v^3\\ z(u,v)=u^2-v^2.\\ \end{array}\right.$$

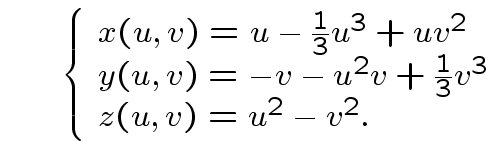
Il complicato oggetto che vediamo sotto, è invece una porzione della superficie minima di Henneberg, di equazioni parametriche

$$\left\{ \begin{array}{l} x(u,v)=-1-\cosh 2u\cos 2v\\ y(u,v)=... ...sinh u\cos v +\frac{1}{3}\sinh 3u\cos 3v.\\ \end{array}\right.$$

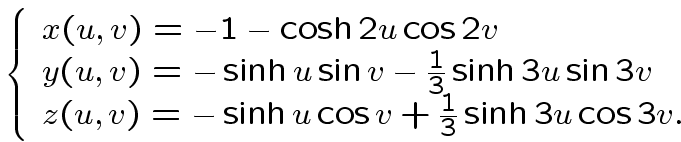
Concludiamo con alcune belle superfici minime periodiche:in alto, la torre di selle di Scherk, di equazione

$$\sin z=\sinh x\sinh y.$$

A sinistra, la superficie di Catalan, di equazioni parametriche

$$\left\{ \begin{array}{l} x(u,v)=1-\cos u\cosh v\\ y(u,v)=4\s... ...h(\frac{v}{2})\\ z(u,v)=u-\sin u\cosh v.\\ \end{array}\right.$$

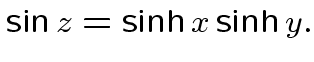
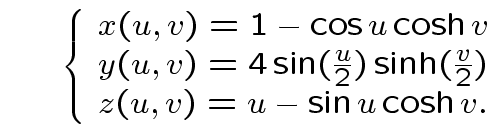
Infine, in basso la prima superficie di Scherk, che è (incredibilmente) un grafico definito su una scacchiera del piano $xy$:

$$z=\log\big(\frac{\cos y}{\cos x}\big).$$

Il figuro accanto alla superficie sono io...