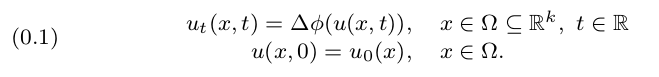Papers

Two nonstandard model for an ill-posed parabolic equation, in preparation.
Abstract:
We study two nonstandard formulations of the Neumann initial value problem

Equations of this form arise in many applications, ranging from the dynamics of aggregating populations to image enhancing. It is well-known that, if ϕ is non-increasing, the aforementioned problem is ill-posed and only has weak solutions in the class of Young measures. Moreover, such solutions are in general not unique. By using nonstandard analysis, we derive from very simple physical principles a fully discrete model and a continuous-in-time and discrete-in-space model for equation 0.1, and we prove that these models are well-posed and formally equivalent to the classical PDE. We then study the properties of these nonstandard models, determining their asymptotic behaviour and other relevant physical properties, chiefly among them an entropy condition that characterizes physically admissible solutions to 0.1. We then exploit the strength of the nonstandard models to discuss the Riemann problem for equation 0.1.


Some applications of numerosities in measure theory (with Vieri Benci and Mauro Di Nasso), Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. vol 26 (2015).
From the introduction:
In this paper we will present three applications of numerosity in topics of measure theory. The first one is about the existence of inner measures associated to any given non-atomic pre-measure. The second application is focused on sets of real numbers. We show that elementary numerosities provide a useful tool with really strong compatibility properties with respect to the Lebesgue measure The third application is about non-Archimedean probability. Following ideas from [1], we consider a model for infinite sequences of coin tosses which is coherent with the original view of Laplace. Moreover, the probability of cylindrical sets exactly coincides with the usual Kolmogorov probability.
[1] V. Benci, L. Horsten, S. Wenmackers (2013), Non-Archimedean probability, vol. 81, pp. 121-151.


Elementary Numerosities and Measures (with Vieri Benci and Mauro Di Nasso), Journal of Logic and Analysis, vol 6 (2014).
Abstract:
Generalizing the notion of numerosity, first introduced in [1], we say that a function n defined on the powerset of a given set X is an elementary numerosity if
1. its range is the non-negative part of a non-archimedean field that extends the field of real numbers;
2. it is finitely additive;
3. n({x}) = 1 for every element x of X.
It turns out that the elementary numerosities are quite general: every non-atomic finitely additive or sigma-additive measure can be obtained as the ratio of an elementary numerosity by a fixed element of F. This theorem can be proved via an ultrapower construction and provides a refinement of a theorem of C. W. Henson about nonstandard representation of measures ([2] Theorem 1). Applications of this result about elementary numerosities will be discussed in a subsequent paper.
[1] V. Benci, M. Di Nasso, Numerosities of labelled sets: a new way of counting, Advances in Mathematics, vol. 173 (2003), pp. 50-67.
[2] C.W. Henson, On the nonstandard representation of measures, Transactions of the American Mathematical Society, vol. 172 (1972), pp. 437-446.


Fermat, Leibniz, Euler, and the gang: the true history of the concepts of limit and shadow (with Tiziana Bascelli, Frederik Herzberg, Vladimir Kanovei, Karin U. Katz, Mikhail G. Katz, Tahl Nowik, David Sherry, and Steven Shnider), Notices of the American Mathematical Society, vol 61, number 8 (2014).
Abstract:
Fermat, Leibniz, Euler, and Cauchy all used one or another form of approximate equality, or the idea of discarding "negligible" terms, so as to obtain a correct analytic answer. Their inferential moves find suitable proxies in the context of modern theories of infinitesimals, and specifically the concept of shadow. We give an application to decreasing rearrangements of real functions.


Omega-Theory: Mathematics with Infinite and Infinitesimal Numbers, thesis under the supervision of Vieri Benci, Mauro Di Nasso and Enrico Vitali (2012).
From the introduction:
Over the last forty years, many attempts have been made in order to simplify the foundational matters and popularize Nonstandard Analysis by means of "easy to grasp" presentations. Following those attempts, the mathematical theories presented in this paper are two simplified version of Nonstandard Analysis expressed in the everyday language of mathematics, in a way to still allow for a complete and rigorous treatment of all the basics of calculus. An important and fascinating feature of those theories lies in the fact that, in contrast with the original formulation of Nonstandard Analysis, their presentation only assumes a few basic notions from algebra, so that they need no more prerequisites than the usual Calculus does. For those reasons, we do believe that Omega-Calculus and its extension given by Omega-Theory are two beautiful and relatively simple theories which could potentially bring many mathematicians, especially those who have no background in logic, closer to the methods of Nonstandard Analysis.
Warning: there are some errors in Section 2.2!