Strutture dati dinamiche: la lista concatenata

Mauro Brunato

Argomenti correlati: [ Strutture dati astratte ] [ La coda ] [ La pila ]

Introduzione

È possibile realizzare strutture dati in grado di allocare memoria solo quand'è necessaria, per ogni singolo dato da memorizzare. Un esempio sono le liste concatenate, in cui ogni elemento è associato a un puntatore contenente l'indirizzo dell'elemento successivo. Nella figura seguente, è rappresentata una lista concatenata avente quattro elementi (detti nodi); la variabile p punta al primo di questi nodi, mentre ciascun nodo contiene un puntatore al nodo successivo. L'ultimo nodo contiene un indirizzo speciale per il puntatore, detto NULL, corrispondente all'indirizzo zero, ad indicare che non punta a nulla.

Dichiarazione e inizializzazione

Se si vuole realizzare una lista concatenata in grado di contenere dei numeri interi, si può dichiarare la seguente struttura:

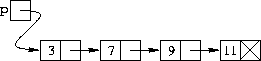
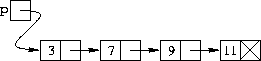
struct nodo {
  int n;
  anagrafica *prossimo;
};

Per rappresentare una lista vuota, poniamo NULL nel puntatore al primo nodo. Quindi, una lista concatenata potrà essere dichiarata come segue:

nodo *p = NULL;

Inserimento di un dato

Supponiamo di voler inserire un nuovo nodo nella lista, contenente ad esempio il numero 1. Ecco una successione di istruzioni che permettono di aggiungere il nodo:

Istruzione	Effetto	Descrizione
`nodo *q = new nodo;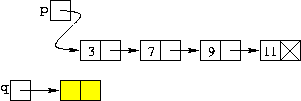`		Creazione del nuovo nodo (in giallo) con l'aiuto di una variabile d'appoggio `q`
`q->n = 1;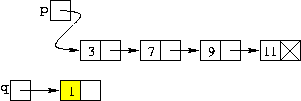`		Scrittura del dato nel nuovo nodo
`q->prossimo = p;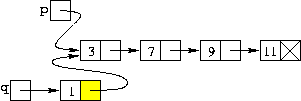`		Concatenazione del nuovo nodo in testa alla lista
`p = q;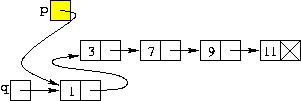`		Dirottamento del puntatore "ufficiale" della lista al nuovo elemento

L'effetto finale di questa sequenza di istruzioni è quello di avere un nodo in più all'inizio della lista, come si vede megli nella seguente figura, dalla quale è stato rimosso il puntatore q, a questo punto ininfluente:

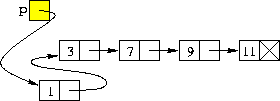
La stessa sequenza di istruzioni funziona anche per inserire il primo elemento in una lista vuota: la verifica è lasciata al lettore.

Stampa del contenuto di una lista

Per stampare il contenuto di una lista è sufficiente realizzare un ciclo in cui, a differenza della scansione di un array, non si incrementa un indice, ma si sposta un puntatore di nodo in nodo:

nodo *q;  // Utilizza un nodo ausiliario
q = p;    // Punta q al primo nodo della lista
while ( q != NULL ) {    // fintantoche' q punta a un nodo (non siamo alla fine della lista)
  cout << q->n << '\n';  // scrivi l'informazione contenuta nel nodo
  q = q->prossimo;       // sposta il puntatore q al prossimo nodo.
}

Più concisamente:

for ( nodo *q = p; q != NULL; q = q->prossimo )
  cout << q->n << '\n';

Eliminazione del primo elemento della lista

Si tratta di effettuare una sorta di "operazione inversa" rispetto all'inserimento. Ripartiamo dalla lista iniziale, quella con quattro elementi, e vediamo come cancellare il primo nodo, contenente l'informazione 3.

Istruzione	Effetto	Descrizione
`nodo *q = p;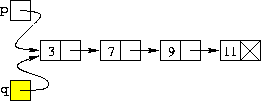`		Salvo l'indirizzo del nodo da eliminare in `q`
`p = p->prossimo;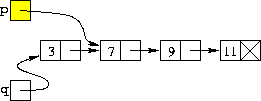`		Avanzamento del puntatore p al nodo che diverrà la nuova testa della lista
`delete q;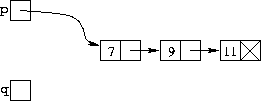`		Cancellazione del nodo da eliminare

Si noti che, disponendo di funzioni per l'inserimento di un elemento in testa alla lista e per la cancellazione di un elemento dalla testa della lista, abbiamo realizzato una struttura di tipo LIFO del tutto equivalente alla pila, senza le limitazioni alle dimensioni dovute all'uso dei vettori.

Inserimento di un elemento in fondo alla coda

Per inserire un nuovo valore, ad esempio 16, in fondo alla coda, dobbiamo dapprima trovare l'ultimo elemento, in modo da concatenare a questo il nuovo nodo. Per farlo abbiamo bisogno di partire dal primo nodo e avanzare finché ci sono nodi successivi. Supponiamo, per ora, che la coda contenga già dei nodi.

Istruzione	Effetto	Descrizione
`nodo *q; for ( q = p; q->prossimo != NULL; q = q->prossimo );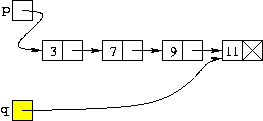`		Ricerca dell'ultimo nodo della lista
`q->prossimo = new nodo;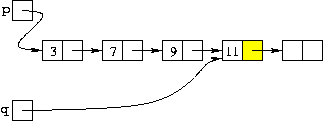`		Creazione del nuovo nodo e assegnazione dell'indirizzo al puntatore che prima era NULL
`q->prossimo->n = 16; q->prossimo->prossimo = NULL;`		Inserimento dei dati nel nuovo nodo

Ovviamente, queste istruzioni non sono valide se la lista è inizialmente vuota; infatti, in questo caso il nuovo nodo non va concatenato a un nodo precedentemente esistente, ma al puntatore p. Il codice diviene il seguente:

if ( p == NULL ) {
  p = new nodo;
  p->n = 16;
  p->prossimo = NULL;
}
else {
  nodo *q;
  for ( q = p; q->prossimo != NULL; q = q->prossimo );
  q->prossimo = new nodo;
  q->prossimo->n = 16;
  q->prossimo->prossimo = NULL;
}

Un altro problema è la necessità di un ciclo per la ricerca dell'ultimo elemento, che può rallentare l'esecuzione del programma se sono richiesti molti inserimenti. Per ovviare a questo, si può definire una lista come un'associazione di due puntatori a nodo, uno verso la testa e uno verso la coda della lista:

struct lista {
  nodo *primo, *ultimo;
};

Una lista definita in questo modo può essere rappresentata come segue:

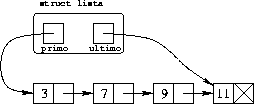
Con il puntatore all'ultimo elemento a disposizione, non è necessario andarlo a cercare ogni volta con un ciclo; per contro, ovviamente tale puntatore dev'essere mantenuto aggiornato, quindi ogni inserimento in coda alla lista richiede la modifica, e anche l'inserimento in testa, se viene eseguito su una lista vuota.

Ricerca di un elemento in una lista

Una lista concatenata non permette l'accesso a qualunque dato a partire da un indice, come nel caso del vettore. Per accedere a un elemento, è necessario partire dall'inizio della lista e procedere di nodo in nodo fino al raggiungimento del nodo giusto. Ad esempio, per cercare il valore n nella lista L servono le seguenti istruzioni:

nodo *q = L.primo;
while ( q != NULL && q->n != n )
  q = q->prossimo;

Alla fine del ciclo, il puntatore q punterà al nodo contenente il dato cercato. Se tale nodo non esiste, q vale NULL.

È chiaro che una strategia come la ricerca binaria non è praticabile. Se la lista è ordinata, è possibile terminare la ricerca non appena si trova un nodo con un valore maggiore di quello cercato. È sufficiente trasformare la condizione "q->n!=n" in "q->n<n".

Inserimento in posizione arbitraria e ordinato

Supponiamo di voler inserire un elemento in una posizione arbitraria della lista. Identifichiamo la posizione per mezzo di un puntatore al nodo che precede la posizione di inserimento.

void inserisci_dopo (lista &L, nodo *p, int n)
{
  nodo *q = new nodo;
  q->n = n;
  q->prossimo = p->prossimo;
  p->prossimo = q;
}

La funzione è in grado di inserire un dato in qualsiasi posizione della lista, tranne in testa, perché è necessario indicare il nodo precedente. Se si adotta la convenzione che l'inserimento in testa è indicato impostando il parametro p a NULL, allora basta gestire il caso particolare all'inizio della funzione. Si noti che la precedente funzione non prende in considerazione l'eventuale aggiornamento del campo ultimo, necessario se la posizione di inserimento è la coda della lista. Lasciamo al lettore la gestione del caso.

Supponiamo ora di voler inserire un elemento in una lista ordinata, mantenendola tale. A meno che non si debba inserire il nuovo elemento in testa alla lista (se è minore di tutti gli elementi già presenti, oppure se la lista è vuota), è necessario individuare il nodo che precede la posizione di inserimento:

void inserisci_ordinato (lista &L, int n)
{
  if ( L.primo == NULL || L.primo->n >= n )  // Se la lista e' vuota o tutti gli elementi sono maggiori di n
    inserisci_dopo (L, NULL, n);             // inserisci in testa alla lista
  else {
    nodo *q = L.primo;                       // punta al primo nodo
    while ( q->prossimo != NULL  && q->prossimo->n < n ) // cerca il nodo che *precede* la posizione corretta per l'inserimento
      q = q->prossimo;
    inserisci_dopo (L, q, n);                // inserisci dopo la posizione trovata.
  }
}

Cancellazione di un elemento arbitrario della lista

Supponiamo che sia dato il puntatore p a un nodo della lista, e che si voglia procedere alla sua eliminazione. Per farlo è necessario accedere al nodo precedente quello da eliminare, allo scopo di dirottare il suo puntatore verso il nodo successivo:

nodo *q = L.primo;
while ( q->prossimo != p )  // Cerca il nodo immediatamente precedente p
  q = q->prossimo;
q->prossimo = p->prossimo;  // Salta il nodo p
delete p;                   // Rilascia la memoria allocata per p.

Il codice precedente non tiene conto del caso particolare in cui il nodo da cancellare si trova in testa alla lista (e quindi non c'è un nodo precedente), e non aggiorna l'eventuale puntatore all'ultimo nodo. Entrambi i casi sono lasciati come esercizi.

Eliminazione dei casi particolari: liste circolari doppiamente concatenate

L'inserimento ordinato sarebbe semplificato se fosse possibile indicare il nodo seguente la posizione di inserimento. Inserire un nodo prima di un nodo dato, però, richiede di tornare indietro lungo la lista, ad esempio inserendo in ciascun nodo un puntatore al nodo precedente:

struct nodo {
  nodo *precedente;
  int n;
  nodo *prossimo;
};

Questa stessa modifica permette, nel caso di cancellazione, di accedere agevolmente al nodo precedente quello da cancellare. Una lista munita di un sistema di puntatori in avanti e all'indietro è detta "doppiamente concatenata". Si noti inoltre che molte delle operazioni sopra definite richiedono la gestione di alcuni casi particolari. L'inserimento nella lista, ad esempio, deve trattare separatamente la testa e, talvolta, la coda. Possiamo fare sì che la testa venga gestita come qualunque altro nodo semplicemente aggiungendo un nodo supplementare, detto "dummy" (fantoccio), oppure "sentinella", senza alcun dato utile al suo interno, il cui puntatore prossimo punta alla vera testa della lista.

Per semplificare l'accesso all'ultimo nodo della lista, possiamo concatenarlo alla sentinella, che diventa quindi un indicatore di "fine della lista". Ecco come si presenta una lista circolare doppiamente concatenata:

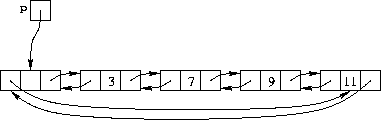
Si noti che la sentinella deve sempre essere presente nella lista, anche se questa è vuota. Una lista vuota è rappresentata come segue:

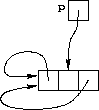
La sentinella è concatenata a sé stessa.

Ecco i files di libreria (header, codice e programma principale) relativi all'uso di una lista circolare doppiamente concatenata.