Esempio - disintegrazione nucleare

Consideriamo in questa sezione un urto anelastico, ma non perfettamente anelastico. Per definizione l'energia cinetica totale non si conserva. Siccome l'energia totale del sistema si conserva sempre (1$^{\textrm{o}}$ principio della termodinamica) parte dell'energia cinetica deve convertirsi in qualche altra forma. Detta $K$ questa parte possiamo scrivere:

$$\frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 = \frac{1}{2} m_1 {v'}_1^2 + \frac{1}{2} m_2 {v'}_2^2 + K$$

Se $K > 0$, una frazione di energia cinetica viene perduta nell'urto, generalmente sotto forma di onde sonore, elettromagnetiche o di calore. Se $K < 0$, una frazione di energia interna al sistema viene convertita in energia cinetica del sistema stesso. Questi urti sono detti talvolta superelastici. Essi sono importanti in fisica atomica e in fisica nucleare, come nel seguente esempio della disintegrazione nucleare dell'uranio $238$:

$$U^{238} \rightarrow \alpha^4 + Th^{234} + \Delta E \quad\quad \textrm{con~} \Delta E = +4.18\textrm{MeV}$$

Il riferimento in cui l'atomo di uranio è fermo ($E^*=0$) è ovviamente quello del centro di massa. La quantità $\Delta E$ è l'energia cinetica dei frammenti dopo l'urto, ovvero $E'^*$. Abbiamo quindi l'uguaglianza $0=E'^* + K$ da cui $K=-E'^*=-4.18$MeV$<0$, cioè la disintegrazione è una specie di ''urto'' superelastico; l'energia addizionale era l'energia di legame fra le due parti che costituivano l'$U^{238}$ prima della disintegrazione.

Siccome qui abbiamo solo due frammenti, le loro quantità di moto sono fissate (in modulo). Svolgeremo i conti nel riferimento del centro di massa, dove le quantità di moto dei frammenti sono indicate come $\vec{q'}_1 = \vec{q}_{Th}$ e $\vec{q'}_2 = \vec{q}_{\alpha}$, ed ovviamente vale la relazione $\vec{q'}_1 = - \vec{q'}_2$: i due frammenti cioè si allontanano in direzioni opposte lungo la stessa retta. Indichiamo con $p_{Th}=p_{\alpha}=p$ i moduli di questi vettori:

$$\Delta E = E'^* = \frac{p^2_{\alpha}}{2m_{\alpha}} + \frac... ...u} \quad\quad \Rightarrow \quad\quad p = \sqrt{2\mu\Delta E}$$

Abbiamo indicato con $\mu = \frac{m_{\alpha}m_{Th}}{m_{\alpha}+m_{Th}}$ la cosiddetta massa ridotta dei due frammenti, che in questo caso vale $\mu=3.93$u.m.a. Si possono ricavare immediatamente anche le energie cinetiche dei singoli frammenti e le loro velocità:

$$\left\{ \begin{array}{lllllllll} {E'}^*_{\alpha} & = & \fr... ...34} & = & 70\cdot 10^{-2}\textrm{MeV} \\ \end{array} \right.$$

$$\left\{ \begin{array}{lllll} {u'}_{\alpha} & = & \frac{p}{... ... & \frac{\sqrt{2\mu\Delta E}}{m_{Th}} \\ \end{array} \right.$$

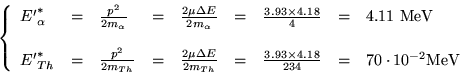
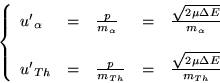
Considerando che $1$u.m.a.$=10^{-27}$Kg$=831$MeV e che $1$eV $=1.6\cdot 10^{19}$J:

$${u'}_{\alpha} \simeq 4 \cdot 10^6 \textrm{m/s} \quad \quad {u'}_{Th} \simeq 6.7 \cdot 10^4 \textrm{m/s}$$