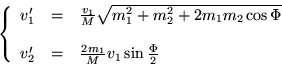Sistema di laboratorio |
Sistema del centro di massa |
Prima dell'urto
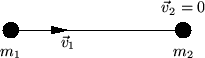
|
Prima dell'urto |
Dopo l'urto
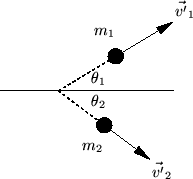
|
Dopo l'urto 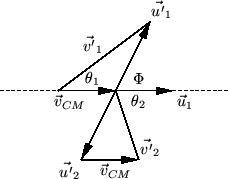
|
Sistema di laboratorio |
Sistema del centro di massa |
Prima dell'urto
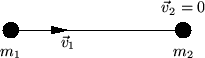
|
Prima dell'urto |
Dopo l'urto

|
Dopo l'urto 
|
L'angolo di scattering ![]() nel centro di massa non ha limitazioni
mentre gli angoli
nel centro di massa non ha limitazioni
mentre gli angoli ![]() e
e ![]() nel sistema di laboratorio
subiscono restrizioni a causa delle leggi di conservazione. Consideriamo
il diagramma relativo all'urto nel centro di massa:
nel sistema di laboratorio
subiscono restrizioni a causa delle leggi di conservazione. Consideriamo
il diagramma relativo all'urto nel centro di massa:
Poichè l'urto è elastico ![]() quindi, dividendo per
quindi, dividendo per ![]() otteniamo:
otteniamo:
Considerando che
![]() e che
e che
![]() si ha:
si ha:
da cui:
![]() ovviamente dipende dai dettagli dell'interazione e, in linea di
principio può assumere qualsiasi valore.
ovviamente dipende dai dettagli dell'interazione e, in linea di
principio può assumere qualsiasi valore. ![]() invece a seconda
del rapporto
invece a seconda
del rapporto
![]() può o non può avere delle limitazioni.
può o non può avere delle limitazioni.
Se ![]() , cioè
, cioè ![]() ,
, ![]() non ha limitazioni,
perchè il denominatore della frazione si può annullare.
Se
non ha limitazioni,
perchè il denominatore della frazione si può annullare.
Se ![]() allora
allora
![]() , ovvero
, ovvero
![]() . Il secondo corpo risente in questo caso
molto poco dell'interazione.
. Il secondo corpo risente in questo caso
molto poco dell'interazione. ![]() si comporta essenzialmente come
un centro di scattering fisso.
si comporta essenzialmente come
un centro di scattering fisso.
Se ![]() , cioè
, cioè ![]() , il denominatore non si può
annullare e
, il denominatore non si può
annullare e ![]() ha un valore massimo
ha un valore massimo ![]() , che si
trova facilmente derivando ed imponendo la derivata uguale a zero:
, che si
trova facilmente derivando ed imponendo la derivata uguale a zero:
Vi è poi il caso particolare ![]()
L'angolo di scattering di laboratorio è la metà dell'angolo
di scattering dal centro di massa. Poichè il valor massimo di
![]() è di
è di ![]() allora se
allora se ![]() l'angolo massimo
di scattering nel sistema di laboratorio non può essere altro
che di
l'angolo massimo
di scattering nel sistema di laboratorio non può essere altro
che di ![]() .
.
Vediamo ora cosa si può dire su ![]() . Dal diagramma
per il moto nel riferimento del centro di massa vediamo
subito che:
. Dal diagramma
per il moto nel riferimento del centro di massa vediamo
subito che:
Procedendo in modo analogo a prima si ricava:
Nel caso del secondo corpo la semplificazione è ora ancora più
banale perchè
![]() , per cui, dividendo per
, per cui, dividendo per ![]() :
:
Se ![]() sappiamo già che:
sappiamo già che:
Infine presentiamo le espressioni di ![]() e
e ![]() in funzione di
in funzione di ![]() e di
e di ![]() .
.