Moto di una particella in un campo di forze centrali

Studiamo il moto di una particella di massa m in un generico campo di forze centrali, descritto dalla funzione energia potenziale . Nota la posizione iniziale, , e la velocità iniziale, , della particella ed il campo di forze determiniamo le equazioni orarie e la traiettoria del moto.

Dato che un campo di forze centrali ha simmetria sferica, è più conveniente esprimere il moto in coordinate polari (Fig. 1). Le equazioni orarie che cerchiamo sono: , , e ; la traiettoria è: .

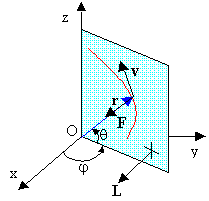
Fig. 1

Un campo di forze centrali è conservativo, per cui l'energia meccanica H della particella, data dalla somma dell'energia cinetica e dell'energia potenziale U(r),

 ,

rimane costante nel tempo e nello spazio. Il suo valore è determinato dalle condizioni iniziali e e vale:

In un campo centrale si conserva anche il momento angolare . Infatti il momento della forza rispetto al centro del campo O, , è nullo dato che forza e raggio vettore sono paralleli; dal fatto che   consegue che si conserva. E così anche è fissato dalle condizioni iniziali e vale:

Dalla conservazione della direzione del momento angolare si deduce che il moto si svolge sempre sul piano definito dai vettori e e quindi, che è costante. Ne consegue che la traiettoria della particella giace sul piano normale alla direzione di (Fig. 1). Dato che è fissato, la equazione della traiettoria sarà perciò una funzione dipendente solo dall'angolo (Fig. 2), cioè:

Esprimendo la velocità nelle componenti radiale e normale al raggio vettore, (Fig. 2), anche l'energia cinetica della particella può essere suddivisa nelle componenti radiale, E_r, e normale, E_q:

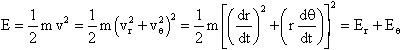
dove, ed .

E_q può essere espressa in funzione del momento angolare L; dimostriamo che . Per far ciò calcoliamo il modulo del momento angolare:

Ricavando la velocità angolare da quest'ultima espressione, e sostituendola in E_q, si ottiene la dipendenza cercata di E_q da L. Si ha così che:

Il termine viene denominato potenziale centrifugo a causa della sua dipendenza da r. L'aggettivo centrifugo è dovuto al fatto che la derivata

è una forza diretta nella stessa direzione del raggio vettore. Sostituendo la (3) nella (1) si ha:

Può sembrare strano che compaia una forza fittizia quando si era partiti con l'analizzare il moto in un riferimento inerziale. Di fatto, la dipendenza di da r implica che il bilancio energetico espresso dall'eq. (4) dipende dalla sola variabile dipendente r, e non da , il che equivale ad analizzare il moto da osservatori non inerziali rotanti con il raggio vettore r. L'energia riportata tra parentesi quadre nell'eq. (4), a causa della dipendenza da r, è detta energia potenziale efficace, U_eff:

U_eff gioca un ruolo importante nella descrizione del moto di una particella in un campo di forze centrali. Un caso particolare è il moto planetario. L'equazione (4) mostra che la componente radiale del moto costituisce un moto unidirezionale nel campo di energia potenziale U_eff.  L'equazione (4) mostra che la componente radiale del moto può essere considerata un semplice moto unidirezionale in un campo di forza di energia potenziale U_eff.
Dalla (4) si ricava che il modulo della velocità radiale v_r = dr/dt è:

dei due segni d'ora in poi prenderemo in considerazione uno dei due segni, per esempio quello positivo, dal momento che il verso di percorrenza della traiettoria è fissato dalle condizioni iniziali, ovvero dalla direzione del momento angolate . I valori di r per i quali il termine tra parentesi tonde

si annulla, determinano i confini del moto per quanto riguarda la distanza dal centro di forza. Infatti se l'uguaglianza (7) è soddisfatta la velocità v_r = dr/dt si annulla. Questo però non vuol dire che la particella si ferma (come di fatto avverrebbe in un moto unidimensionale) dal momento che la velocità angolare dq/dt non può annullarsi se L è diverso da zero (eq. (2)). L'uguaglianza v_r = dr/dt = 0 comporta un punto di svolta della traiettoria in cui r(t) da crescente diventa decrescente o viceversa (vedi diagrammi dell'energia).
L'equazione oraria r = r(t) si ricava dall' eq. 6 per semplice separazione delle variabili r e t :

Integrando tra la posizione iniziale r₀ al tempo t₀ = 0, e la posizione r nel generico istante t, si ha:

Sostituendo nell'eq. 9 la funzione energia potenziale che descrive il campo di forza, e risolvendo l'integrale si ottiene l'equazione r = r(t).

Nota la r = r(t), l'equazione oraria q = q(t) si ottiene sostituendo nell'eq. 2 la funzione r(t) e separando le variabili q e t:

Integrando tra la posizione angolare iniziale q₀ e la posizione q al generico istante t, si ricava l'equazione oraria q = q(t):

Ancora una volta, l'integrale a primo membro potrà essere risolto nota la funzione U = U(r); nel seguito porteremo come esempio il caso del potenziale gravitazionale.
L'equazione della traiettoria si ottiene osservando che la velocità radiale può essere scritta come:

Sostituendo nell'eq.12 la velocità radiale (eq. 6) e la velocità angolare dq/dt ricavabile dall'eq.2, si ha:

da cui, separando le variabili r e q si ottiene:

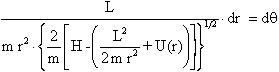
e, integrando si ha:

Inserendo nell'eq. 14 la funzione energia potenziale ed integrando si ottiene finalmente l'equazione della traiettoria in coordinate polari r = r(q).

Come vedremo analizzando i diagrammi dell'energia, la variazione di r nel tempo ed in funzione di q, a seconda delle condizioni iniziali, può essere vincolata alla condizione , o alla condizione . Nel primo caso la traiettoria della particella è sicuramente aperta, essa proviene dall'infinito e torna all'infinito. Nel secondo caso (Fig. 3) il moto è finito e la traiettoria giace in una corona circolare delimitata dalle circonferenze aventi raggi: r_min ed r_max. Ciò però non significa che la traiettoria sia necessariamente chiusa. Nell'intervallo di tempo in cui r varia da r_max ad r_min e di nuovo ad r_max il raggio vettore ruota di un angolo Dq ottenibile dall'eq. 14 è: