


Next: Dissipazione della potenza di
Up: Effetti di smorzamento nel
Previous: Decadimento dell'energia nel regime
Indice
Il regime di forte smorzamento si instaura quando
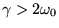 ;
in questo caso le soluzioni del polinomio caratteristico associato
all'equazione differenziale del moto sono entrambe reali negative:
;
in questo caso le soluzioni del polinomio caratteristico associato
all'equazione differenziale del moto sono entrambe reali negative:
È consuetudine definire
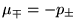 così da poter
lavorare con quantità positive. Si noti che le
così da poter
lavorare con quantità positive. Si noti che le 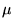 sono una
maggiore ed una minore di
sono una
maggiore ed una minore di 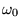 e che il loro prodotto vale
e che il loro prodotto vale
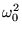 :
:
Passiamo ora alla legge del moto; la forma più generale di 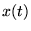 è
una sovrapposizione di due esponenziali con lunghezze caratteristiche
è
una sovrapposizione di due esponenziali con lunghezze caratteristiche
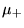 e
e 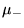 . I coefficienti devono essere reali per evitare che
. I coefficienti devono essere reali per evitare che
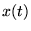 sia complesso:
sia complesso:
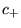 e
e 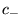 sono determinati dalle condizioni iniziali, mentre
sono determinati dalle condizioni iniziali, mentre
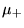 e
e 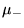 dipendono dalle proprietà fisiche dell'oscillatore.
Vi sono a questo punto due casi: se
dipendono dalle proprietà fisiche dell'oscillatore.
Vi sono a questo punto due casi: se 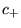 e
e 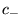 hanno lo stesso segno,
allora
hanno lo stesso segno,
allora 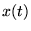 non si annulla mai, quindi il sistema non passa mai per
la posizione di equilibrio. Viceversa, se i due coefficienti hanno segno
diverso
non si annulla mai, quindi il sistema non passa mai per
la posizione di equilibrio. Viceversa, se i due coefficienti hanno segno
diverso 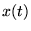 può annullarsi (quando i due esponenziali si annullano
l'un l'altro) ed il sistema può passare per la posizione di equilibrio
(una sola volta però). I due casi sono rappresentati nella figura seguente:
può annullarsi (quando i due esponenziali si annullano
l'un l'altro) ed il sistema può passare per la posizione di equilibrio
(una sola volta però). I due casi sono rappresentati nella figura seguente:
Per le condizioni iniziali 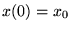 ed
ed 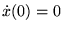 abbiamo
abbiamo
risolvendo rispetto a 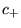 e
e 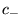 otteniamo infine una soluzione
che dipende solo da
otteniamo infine una soluzione
che dipende solo da 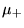 e
e 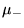 (questo ovviamente viene dal
fatto che abbiamo fissato le condizioni iniziali):
(questo ovviamente viene dal
fatto che abbiamo fissato le condizioni iniziali):



Next: Dissipazione della potenza di
Up: Effetti di smorzamento nel
Previous: Decadimento dell'energia nel regime
Indice
Stefano Bettelli
2002-09-10
![]() così da poter
lavorare con quantità positive. Si noti che le
così da poter
lavorare con quantità positive. Si noti che le ![]() sono una
maggiore ed una minore di
sono una
maggiore ed una minore di ![]() e che il loro prodotto vale
e che il loro prodotto vale
![]() :
:
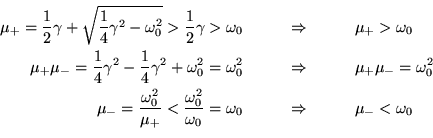
![]() è
una sovrapposizione di due esponenziali con lunghezze caratteristiche
è
una sovrapposizione di due esponenziali con lunghezze caratteristiche
![]() e
e ![]() . I coefficienti devono essere reali per evitare che
. I coefficienti devono essere reali per evitare che
![]() sia complesso:
sia complesso:
![\includegraphics[width=.8\linewidth]{smorz-due.eps}](img134.png)
![]() ed
ed ![]() abbiamo
abbiamo
![]() e
e ![]() otteniamo infine una soluzione
che dipende solo da
otteniamo infine una soluzione
che dipende solo da ![]() e
e ![]() (questo ovviamente viene dal
fatto che abbiamo fissato le condizioni iniziali):
(questo ovviamente viene dal
fatto che abbiamo fissato le condizioni iniziali):