Relazione fra energia immagazzinata e vita media dell'oscillatore

Vogliamo ora vedere la relazione fra l'energia totale immagazzinata in media da un oscillatore armonico forzato e smorzato, in condizioni di piccolo smorzamento ed a regime, e la vita media $\tau$ dell'oscillatore stesso. L'energia totale media dell'oscillatore scritta come somma dell'energia cinetica e dell'energia potenziale elastica, diventa (ricordare l'espressione (3) per il valore di $A$):

$$\begin{eqnarray*} \ensuremath{\langle H \rangle}& = & \frac{1}{2}m\omega_0^2\e... ...{(\omega_0^2-\omega^2)^2 + \left( \frac{\omega}{\tau} \right)^2} \end{eqnarray*}$$

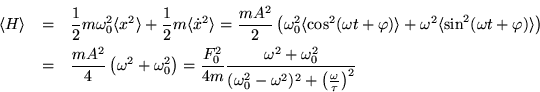
Vediamo dunque che il grafico di $\ensuremath{\langle H(\omega) \rangle}$ è una curva che raggiunge il massimo per $\omega=\omega_0$. In condizioni di piccolo smorzamento la curva è molto stretta e piccata in corrispondenza di $\omega=\omega_0$, ed è altrove praticamente nulla. Questo permette di approssimare $\omega$ con $\omega_0$ nella sua espressione, tranne che nel termine $(\omega_0^2-\omega^2)^2$ perchè questo, in vicinanza della risonanza $\omega_0$, varia moltissimo. Possiamo però riscrivere la differenza di due quadrati come il prodotto della somma e della differenza delle basi, quindi:

$$\omega_0^2 - \omega^2 = (\omega_0 + \omega)(\omega_0 - \omega) \sim 2\omega_0 (\omega_0 - \omega)$$

Applicando queste approssimazioni otteniamo infine che l'energia totale media dell'oscillatore segue l'andamento di una funzione lorentziana:

$$\ensuremath{\langle H \rangle}= \frac{F_0^2}{4m} \frac{2\om... ...{F_0^2}{8m} \frac{1} {(\omega-\omega_0)^2 + \frac{1}{4\tau^2}}$$

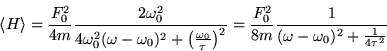
Il valor massimo di $\ensuremath{\langle H \rangle}$ si ottiene ovviamente quando il denominatore è minimo, ovvero per $\omega=\omega_0$, quindi: $$\ensuremath{\langle H \rangle}_{max} = \frac{F_0^2\tau^2}{2m}$$ L'espressione dell'enegia si può allora riscrivere inglobando tutte le dimensioni in $\ensuremath{\langle H \rangle}_{max}$, e riservando un termine puramente numerico per esprimere la forma della curva: $$\ensuremath{\langle H \rangle}= \frac{\ensuremath{\langle H \rangle}_{max}}{1 + 4\tau^2(\omega-\omega_0)^2}$$

Da qui è facile calcolare quando l'energia diventa metà del suo valor massimo, infatti:

$$\ensuremath{\langle H \rangle}= \frac{1}{2} \ensuremath{\la... ...uad\quad} \omega = \omega_0 \pm \frac{1}{2\tau} = \omega_{\pm}$$

La larghezza della curva a mezza altezza (in inglese ``full width at half maximum'' o FWHM) risulta quindi essere uguale a $\Delta\omega_{\frac{1}{2}} = \omega_+ - \omega_- = 1/\tau$ Poichè $1/\tau = \gamma$, vediamo immediatamente che più piccolo è il coefficiente di attrito e più stretta è la curva. In modo analogo, ricordando che il fattore di merito $Q$ è definito come $\omega_0\tau$, vediamo che la curva è tanto più stretta quanto più grande è $Q$.