Il teorema di Carnot generalizzato

Giuseppe Dalba

In questi appunti vogliamo dimostrare che il rendimento di una macchina termica che lavori a contatto con infinite sorgenti fra una temperatura massima $\ensuremath{T_{+}}$ ed una minima $\ensuremath{T_{-}}$ è sempre minore del rendimento di una macchina di Carnot che lavori nello stesso intervallo di temperatura. Consideriamo il ciclo reversibile $M$ mostrato in figura, che lavora a contatto con un gran numero di sorgenti, la temperatura essendo compresa nell'intervallo $[\ensuremath{T_{-}}, \ensuremath{T_{+}}]$, ed il corrispondente ciclo $C$ di Carnot.

L'integrale di Clausius (ovvero l'integrale degli scambi di calore divisi per la temperatura a cui avvengono) per il ciclo termodinamico $M$, che è reversibile per ipotesi, è sicuramente nullo. Possiamo dividere questo integrale in due parti, $A$ e $B$, nelle quali rispettivamente si assorbe o si cede solo calore:

$$0 = \oint \frac{\omega}{T} = \underbrace{\int_A \frac{\ver... ...erbrace{\int_B \frac{\vert\omega\vert}{T}}_{\textrm{cessione}}$$

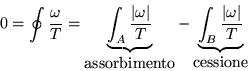
Possiamo minorare il primo integrale sostituendo $\ensuremath{T_{+}}$ al posto della temperatura a cui lo scambio di calore avviene. Allo stesso modo possiamo rimpiazzare $T$ nel secondo integrale con $\ensuremath{T_{-}}$ ed ottenere un valore più grande. A questo punto le temperature possono essere portate fuori dal segno di integrazione, e $\int \omega$ si riduce semplicemente al calore assorbito $\ensuremath{Q_{+}}$ o ceduto $\ensuremath{Q_{-}}$. Siccome il secondo integrale ha un segno negativo, in entrambi i casi stiamo sottovalutando l'integrale di Clausius, quindi;

$$0 = \oint \frac{\omega}{T} > \frac{\vert\ensuremath{Q_{+}}... ...-}}} > \frac{\vert\ensuremath{Q_{+}}\vert}{\ensuremath{T_{+}}}$$

Questa relazione ci permette immediatamente di ricavare una disuguaglianza fra il rendimento del ciclo $M$ e quello della corrispondente macchina di Carnot (che è $\eta_C = 1 - \ensuremath{T_{-}}/\ensuremath{T_{+}}$):

$$\frac{\vert\ensuremath{Q_{-}}\vert}{\vert\ensuremath{Q_{+}}... ...ce{1 - \frac{\ensuremath{T_{-}}}{\ensuremath{T_{+}}}}_{\eta_C}$$

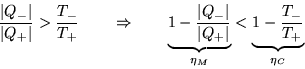
il che è equivalente a scrivere appunto $\eta_M < \eta_C$, come volevasi dimostrare. Quindi una macchina termica il cui fluido di lavoro subisca un ciclo reversibile scambiando calore con infinite sorgenti a temperatura compresa fra un valore minimo $\ensuremath{T_{-}}$ ed uno massimo $\ensuremath{T_{+}}$ ha rendimento inferiore alla machina di Carnot che utilizza sorgenti fra le stesse temperature estreme. Se la macchina termica $M$ fosse una macchina reale, e pertanto irreversibile, il suo rendimento sarebbe minore di quello della corrispondente machina reversibile e quindi, a maggior ragione sarebbe minore del rendimento della macchina di Carnot che utilizza le sorgenti a temperatura $\ensuremath{T_{+}}$ e $\ensuremath{T_{-}}$.