Moto dei razzi

Giuseppe Dalba

In questi appunti vogliamo determinare la legge $v(t)$ con cui varia la velocità di un razzo. Bisognerà tenere conto che la massa del razzo viene usata per la sua propulsione, quindi essa diminuisce nel tempo. Assumeremo che la massa espulsa dal razzo abbia una velocità $u$ indipendente dal tempo, al momento dell'espulsione, rispetto ad un riferimento $O'$ solidale con il razzo:

Per risolvere il problema assumeremo che il razzo espella i gas di scarico da cui è spinto in quantità discrete $dm$ ad intervalli regolari, ai tempi $t$, $t+dt$, $t+2dt$ ...La soluzione del problema si avrà passando al limite per $dt \to 0$. Fra due espulsioni successive i gas ed il razzo procedono di moto rettilineo uniforme.

Per fissare le idee, diciamo che all'istante $t$ la velocità del razzo passa repentinamente da $v$ a $v+dv$ a causa dell'espulsione della massa $dm$. Quindi, nell'intervallo $[t,t+dt]$ l'impulso del razzo è $p_R = (m-dm)(v+dv)$ (rispetto al riferimento di laboratorio $O$). Sempre rispetto al laboratorio, l'impulso del gas è

$$p_G = dm ( v + dv - u )$$

Nel suo complesso, il sistema gas-razzo non può avere modificato il suo impulso totale rispetto al laboratorio, quindi possiamo scrivere la seguente identità:

$$mv = p(t) = p(t+dt) = p_R + p_G = (m-dm)(v+dv) + dm(v+dv-u) = mv + m\,dv - u\,dm$$

$$\ensuremath{\quad\quad \Rightarrow \quad\quad}m\,dv = u\,dm$$

Questa è una relazione differenziale fra la variazione di velocità e la variazione di massa. Integrando otteniamo:

$$dv = u\frac{dm}{m} \ensuremath{\quad\quad \Rightarrow \qua... ... u \int_{m(t_0)}^{m(t)} \frac{dm}{m} = u \ln \frac{m(t)}{m_0}$$

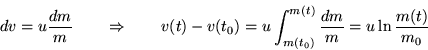
Se scegliamo come istante iniziale quello in cui il razzo era fermo avremo $v_0 = 0$ e $m_0=M$ (la massa totale del razzo alla partenza, con tutto il carburante al suo interno). Chiamiamo $\mu=\frac{1}{M} \frac{dm}{dt}$ il tasso relativo di espulsione del carburante. Allora la massa del razzo, per gli assunti precedenti, diminuirà linearmente nel tempo secondo la relazione $m(t)=M(1-\mu t)$. La legge precedente diventa allora:

$$v(t) = u \ln \frac{m(t)}{M} = u \ln (1-\mu t)$$