Soluzioni di esercizi sulla dinamica dei sistemi

Esercizio 1
Dopo che il proiettile si è conficcato nel blocco, i due corpi diventano un corpo solo di massa e la velocità istantanea appena dopo sarà determinata dalla conservazione della quantità di moto:

$\begin{displaymath} \frac{m}{4}v = m'v' \quad\quad \rightarrow \quad\quad v' ... ...arrow \quad\quad E = \frac{1}{2}m'{v'}^2 = \frac{1}{40}mv^2 \end{displaymath}$

A questo punto le due molle cominciano ad essere compresse. Se indichiamo con ed l'entità della compressione, otteniamo che le forze elastiche delle due molle sono rispettivamente e . Ora queste due forze devono essere uguali per la condizione di azione e reazione nel punto di contatto fra le due molle. Possiamo allora esprimere in funzione di , o meglio entrambe in funzione della somma :

$\begin{displaymath} k_1x_1=k_2x_2 \quad\quad \rightarrow \quad\quad x_2 = x_1\... ...uad\quad x = x_1 + x_2 = x_1\left(1 + \frac{k_1}{k_2}\right) \end{displaymath}$

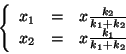
$\begin{displaymath} \left\{ \begin{array}{lll} x_1 & = & x\frac{k_2}{k_1+k_2} \\ x_2 & = & x\frac{k_1}{k_1+k_2} \\ \end{array} \right. \end{displaymath}$

La forza esercitata sul blocco sarà allora:

$\begin{displaymath} F = k_2x_2 = x\frac{k_1k_2}{k_1+k_2} = kx \quad\quad \textrm{dove~} k = \frac{k_1k_2}{k_1+k_2} \end{displaymath}$

Il blocco di massa complessiva incontra quindi una resistenza identica a quella esercitata da un'unica molla di costante elastica . È a questo punto ovvio che la velocità massima è quella iniziale () e che spostamento massimo e pulsazione di oscillazione sono quelli dati dalle leggi del moto armonico $x(t)=\frac{v'}{\omega}\sin(\omega t)$ :

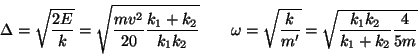
$\begin{displaymath} \Delta = \sqrt{\frac{2E}{k}} = \sqrt{\frac{mv^2}{20}\frac{... ...t{\frac{k}{m'}} = \sqrt{\frac{k_1k_2}{k_1+k_2}\frac{4}{5m}} \end{displaymath}$

Esercizio 2
Facciamo alcune posizioni per visualizzare meglio il problema. Consideriamo un riferimento inerziale, la cui origine è posta al centro dell'asta (prima dell'urto). Il punto materiale ha inizialmente velocità $v\hat{x}$ e collide con l'asta al tempo zero nel punto $-h\hat{y}$ , e questo definisce tutto del nostro sistema di riferimento. Dopo l'urto il punto materiale si muoverà di moto rettilineo uniforme con velocità diversa da prima, di modulo in direzione $\hat{q}=\hat{x}\cos\alpha- \hat{y}\sin\alpha$ . La sua legge del moto sarà dunque:

$\begin{displaymath} \vec{R}(t) = -h\hat{y} + vt\hat{x} \quad \textrm{per $t<0$}... ... \vec{R}(t) = -h\hat{y} + v't\hat{q} \quad \textrm{per $t>0$} \end{displaymath}$

Il centro di massa dell'asta si muoverà invece (dopo l'urto) con velocità in direzione $\hat{Q}=\hat{x}\cos\beta+ \hat{y}\sin\beta$ , e la velocità angolare dell'asta nel riferimento del suo centro di massa sarà $\omega\hat{z}$ . Per determinare tutte queste quantità abbiamo a disposizione la conservazione della quantità di moto sul piano, la conservazione del momento angolare rispetto ad un punto qualsiasi (per esempio l'origine del riferimento) e la conservazione dell'energia (poichè l'urto è anelastico). Riassumendo:

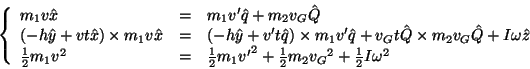
$\begin{displaymath} \left\{ \begin{array}{lll} m_1v\hat{x} & = & m_1v'\hat{q} ... ...{2}m_2{v_G}^2 + \frac{1}{2}I\omega^2 \\ \end{array} \right. \end{displaymath}$

dove è il momento di inerzia di un'asta di lunghezza rispetto al suo centro di massa, ovvero $\frac{1}{12}m_2d^2$ . Consideriamo ora la relazione di conservazione del momento angolare e sopprimiamo i termini nulli $\hat{x}\times\hat{x}$ e simili. Otteniamo:

$\begin{displaymath} -h m_1 v\hat{y}\times\hat{x} = -h m_1 v'\hat{y}\times\hat{q} + I\omega\hat{z} \end{displaymath}$

Siccome $\hat{y}\times\hat{x}=-\hat{z}$ e $\hat{y}\times\hat{q}=-\hat{z}\cos\alpha$ , questa si semplifica nella seguente equazione scalare:

$\begin{displaymath} h m_1 (v - v'\cos\alpha) = I\omega \end{displaymath}$

Passiamo alla conservazione della quantità di moto e decomponiamo $\hat{q}$ ed $\hat{Q}$ lungo gli assi coordinati:

$\begin{displaymath} \left\{ \begin{array}{lll} m_1v & = & m_1v'\cos\alpha + m_... ...& -m_1v'\sin\alpha + m_2v_G\sin\beta \\ \end{array} \right. \end{displaymath}$

Riassumendo, ci siamo ridotti al seguente sistema di quattro equazioni in cinque incognite (, , $\omega$ , $\alpha$ e $\beta$ ):

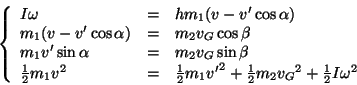
$\begin{displaymath} \left\{ \begin{array}{lll} I\omega & = & h m_1 (v - v'\cos... ...{2}m_2{v_G}^2 + \frac{1}{2}I\omega^2 \\ \end{array} \right. \end{displaymath}$

Questo sistema non si può ovviamente risolvere senza una ulteriore ipotesi fisica, ovvero che le superfici del punto materiale e dell'asta nel punto di contatto non siano scabre. Questo implica che le forze esercitate dall'uno sull'altra e viceversa siano tutte dirette lungo l'asse , quindi che il moto del punto materiale rimane lungo l'asse e che $\alpha=0$ . Imponendo questa condizione vediamo immediatamente che anche l'angolo $\beta$ deve essere nullo, ed il sistema si semplifica in:

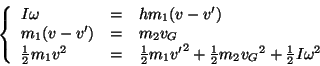
$\begin{displaymath} \left\{ \begin{array}{lll} I\omega & = & h m_1 (v - v') \\... ...{2}m_2{v_G}^2 + \frac{1}{2}I\omega^2 \\ \end{array} \right. \end{displaymath}$

La terza equazione è sparita perchè i due membri sono identicamente nulli; ora abbiamo tre equazioni in tre incognite e possiamo passare a risolvere. Sostituendo la seconda nella terza abbiamo $I\omega = h m_2v_G$ , e la conservazione dell'energia diventa:

$\begin{displaymath} m_1v^2 = m_1(v - \frac{I\omega}{hm_1})^2 + m_2(\frac{I\omega}{hm_2})^2 + I\omega^2 \end{displaymath}$

Eliminando a primo e secondo membro il termine abbiamo tutti termini proporzionali a $I\omega$ che non può essere nullo. Semplificandolo otteniamo:

$\begin{displaymath} \frac{2v}{h} = \frac{I\omega}{h^2}(\frac{1}{m_1} + \frac{1... ...c{I\omega}{h}(\frac{1}{m_1} + \frac{1}{m_2} + \frac{h^2}{I}) \end{displaymath}$

Il termine fra parentesi tonde ha le dimensioni di un inverso di una massa. Poniamo allora $M=(\frac{1}{m_1} + \frac{1}{m_2} + \frac{h^2}{I})^{-1}$ ed otteniamo $2Mhv = I\omega$ che risolve il problema per $\omega$ . Per sostituzione otteniamo immediatamente il valore di tutte le altre quantità:

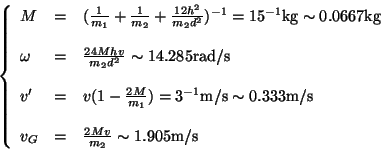
$\begin{displaymath} \left\{ \begin{array}{lll} M & = & (\frac{1}{m_1} + \frac{... ...rac{2Mv}{m_2} \sim 1.905\textrm{m/s} \\ \end{array} \right. \end{displaymath}$

Le velocità come direzione sono $\vec{v'}=v'\hat{q}=v'\hat{x}$ e $\vec{v_G}=v_G\hat{Q}=v_G\hat{x}$ . Il moto del punto materiale verrebbe invertito quando risultasse ovvero $m_1<2M\sim 0.133$ kg.

Esercizio 3

a) La velocità con cui la massa m raggiunge la molla è la stessa con cui arriva alla fine del piano inclinato; infatti nel piano orizzontale non c’è attrito.

Dunque:

con

da cui

La compressione della molla:

E_cinetica=E_elastica

da cui si ricava:

b) La molla trasferisce l’energia ricevuta come energia cinetica. Il bilancio energetico tra inizio e fine può essere fatto senza considerare energia elastica né quella cinetica. Infatti tutta l’energia potenziale iniziale mgh si trasforma in energia potenziale mgh’ e lavoro della forza d’attrito.

Dunque:

ricordando che

si ottiene:

c) L’energia dissipata per attrito è:

Esercizio 4
a) Un satellite geostazionario ha un periodo di rivoluzione di 24 ore: T = 86400 s
Nel sistema di riferimento del satellite forza centrifuga e forza gravitazionale si equivalgono:

dove

e quindi:

da cui si ottiene h = 3.6 x 10⁷ m

b) La velocità del satellite è

c) L’energia del satellite sarà la somma della sua energia cinetica e di quella gravitazionale (potenziale):

a) L’energia che devono erogare i motori sarà proprio l’energia di legame del punto c).

Esercizio 5

a) Non essendoci attriti si conserva sia l’energia meccanica che la quantità di moto (solo lungo x, visto che lungo y agisce la forza di gravità).

Nell’istante iniziale:

Nell’istante in cui raggiunge la quota massima sulla rampa:

(nell’istante in cui m₁ raggiunge la quota mazzima h la pallina è ferma rispetto alla rampa ma si muove a velocità v con la rampa rispetto al riferimento solidale con il tavolo)

Dalla conservazione della quantità di moto lungo x () si ottiene

Dalla conservazione dell’energia meccanica () si ottiene:

b) Consideriamo ora quantità di moto ed energia dopo la discesa dalla rampa.

Dalla conservazione della quantità di moto lungo x () e dell’energia meccanica () si ottiene

c) Per si ha: e

Per si ha: e

Esercizio 6
Risolveremo questo problema utilizzando la conservazione dell'energia piuttosto che la dinamica del sistema. Chiamiamo e le velocità (in modulo) del piano inclinato e del blocco rispettivamente, rispetto ad un sistema di riferimento solidale con la superficie orizzontale (un riferimento inerziale). La velocità del piano inclinato sarà puramente orizzontale, cioè $\vec{v}_M = - v_M \hat{x}$ , mentre quella del blocco avrà una componente anche lungo la verticale. Attenzione: la componente orizzontale di $\vec{v}_m$ NON è $v_m\cos\alpha$ , poichè il piano inclinato scivola sotto il blocco quindi il blocco non scende seguendo una inclinazione $\alpha$ . Il bilancio energetico all'istante finale, cioè quando , (tralasciando di scrivere l'energia potenziale del piano inclinato che non cambia, perchè questo si muove solo in orizzontale) impone:

$\begin{displaymath} mgh = \frac{1}{2}Mv_M^2 + \frac{1}{2}mv_m^2 \end{displaymath}$

Nonostante compaiano due variabili, questo problema è unidimensionale perchè le due variabili non sono indipendenti. Per mostrarlo le scriveremo entrambe in funzione della velocità del blocco rispetto al piano inclinato. La relazione fra e è abbastanza semplice se conosciamo :

$\begin{displaymath} \vec{v}_m\vert _x = v'\cos\alpha - v_M \neq v_m\cos\alpha \quad\quad \vec{v}_m\vert _y = v'\sin\alpha \end{displaymath}$

La relazione fra e si trova ora imponendo la conservazione dell'impulso lungo $\hat{x}$ : infatti non vi sono forze esterne al sistema piano inclinato - blocco con componente non nulla lungo l'asse orizzontale:

$\begin{displaymath} Mv_M = m\vec{v}_m\vert _x = mv'\cos\alpha - mv_M \quad\quad \rightarrow \quad\quad v_M = \frac{m}{m+M}v'\cos\alpha \end{displaymath}$

Le considerazioni precedenti ci permettono ora di scrivere tutto in funzione di :

$\begin{displaymath} mgh = \frac{1}{2}\frac{Mm^2}{(m+M)^2}v'^2\cos^2\alpha + \f... ...a - \frac{m}{m+M}v'\cos\alpha)^2 + v'^2\sin^2\alpha \right) \end{displaymath}$

Dopo noiose semplificazioni ci riduciamo a:

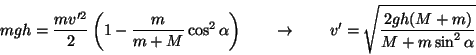
$\begin{displaymath} mgh = \frac{mv'^2}{2}\left(1 - \frac{m}{m+M}\cos^2\alpha\ri... ...rrow \quad\quad v' = \sqrt{\frac{2gh(M+m)}{M+m\sin^2\alpha}} \end{displaymath}$

Da cui ricaviamo le velocità e che sono l'oggetto del problema:

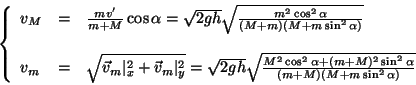
$\begin{displaymath} \left\{ \begin{array}{lll} v_M & = & \frac{mv'}{m+M}\cos\a... ...^2\alpha} {(m+M)(M+m\sin^2\alpha)}} \\ \end{array} \right. \end{displaymath}$

Esercizio 7
La palla da biliardo è soggetta solo alla forza di attrito di modulo costante $\mu mg$ in direzione opposta al moto del centro di massa della palla. Questa forza esercita un momento rispetto al centro della palla pari a $\mu mgR$ che determina la variazione $I\dot{\omega}$ del momento angolare (ricordiamo che per una sfera omogenea il momento di inerzia rispetto al centro è $\frac{2}{5}mR^2$ ). Quindi:

$\begin{displaymath} \mu mgR = \frac{2}{5}mR^2\dot{\omega} \quad\quad \rightarr... ...quad\quad \omega(t) = \omega_0 + \frac{5}{2}\frac{\mu gt}{R} \end{displaymath}$

Inoltre per ipotesi $\omega_0 = 0$ cioè la palla non ha velocità angolare inizialmente. La velocità lineare del centro di massa della palla da biliardo inoltre decresce linearmente nel tempo perchè la decelerazione $\mu mg$ è costante:

$\begin{displaymath} v(t) = v_0 - \mu mgt \end{displaymath}$

La condizione di non strisciamento si raggiunge quando la velocità del punto di contatto fra palla e superficie è nulla:

$\begin{displaymath} v_P = v(t_f) - R\omega(t_f) = 0 \quad\quad \rightarrow \qu... ...ad \rightarrow \quad\quad t_f = \frac{2}{7}\frac{v_0}{\mu g} \end{displaymath}$

Per sostituzione si ricava la velocità lineare al tempo :

$\begin{displaymath} v_f = v(t_f) = v_0 - \frac{2}{7}v_0 = \frac{5}{7}v_0 \end{displaymath}$

Infine, lo spazio percorso dal centro di massa si ricava dalla legge dei moti uniformemente decelerati:

$\begin{displaymath} s = v_0 t_f - \frac{1}{2}\mu g t_f^2 = \frac{2}{7}\frac{v_... ...2}{49}\frac{v_0^2}{\mu g} = \frac{12}{49}\frac{v_0^2}{\mu g} \end{displaymath}$

Esercizio 8
Calcoliamo intanto il momento di inerzia del sistema asta e pallina rispetto all'asse di rotazione nel caso di urto totalmente anelastico (quando cioè la pallina rimane conficcata nell'asta ad una distanza $\Delta=h+d/2$ dall'asse di rotazione):

$\begin{displaymath} I' = I + m'\Delta^2 = I_0 + \frac{md^2}{4} + m'\Delta^2 = ... ...d^2}{3}\left( 1 + 3\frac{m'}{m}\frac{\Delta^2}{d^2} \right) \end{displaymath}$

Il secondo termine in parentesi è estremamente piccolo (vale circa quando si sotituiscono i valori numerici). Per semplificare i conti supporremo di poterlo trascurare, ovvero stiamo assumendo che $I' \sim I = \frac{md^2}{3}$ . Imponiamo ora la conservazione del momento angolare rispetto all'asse di rotazione per ricavare la velocità angolare un istante dopo l'impatto:

$\begin{displaymath} m'v\Delta = I'\omega \quad\quad \rightarrow \quad\quad \om... ...= \frac{m'v\Delta}{I'} \sim \frac{3v\Delta}{d^2}\frac{m'}{m} \end{displaymath}$

In questo caso naturalmente il rapporto , seppur piccolo, è l'unico termine in gioco e non può essere trascurato. Scegliendo il centro dell'asta come riferimento per l'asse verticale, il centro di massa del sistema asta più pallina si trova ad altezza:

$\begin{displaymath} y' = \frac{-hm'}{m+m'} \sim -h\frac{m'}{m} \ll \frac{d}{2} \textrm{~~(in modulo!)} \end{displaymath}$

Siccome stiamo già trascurando i termini piccoli in $\frac{m'}{m}$ approssimiamo anche cioè confondiamo il centro di massa del sistema con il centro dell'asta. Ora è facile calcolare di quanto si alza il centro dell'asta nel caso di urto totalmente anelastico imponendo la conservazione della energia:

$\begin{displaymath} \frac{1}{2}I\omega^2 \sim mg\delta \quad\quad \rightarrow ... ... \sim \frac{3v^2\Delta^2m'^2}{2gd^2m^2} \sim 4.2\textrm{cm} \end{displaymath}$

Il risultato naturalmente è approssimato a meno di termini piccoli in $\frac{m'}{m}$ . Un calcolo esatto porterebbe a $\delta \sim 4.05$ cm. Passiamo ora al caso di urto elastico: in questo caso la velocità della pallina dopo l'urto è una variabile indipendente, ma la conservazione dell'energia vale durante la collisione. Ponendo ancora $\Delta=h+d/2$ e sapendo che (questa volta in modo esatto), otteniamo:

$\begin{displaymath} \left\{ \begin{array}{llll} m'v\Delta & = & I\omega + m'v'... ...ac{1}{2}m'v'^2 & \textrm{~~energia} \\ \end{array} \right. \end{displaymath}$

Dalla prima equazione possiamo ricavare $\omega$ e sostituirlo nella seconda, che può poi essere risolta rispetto a . Tralasciando i passaggi banali ma noiosi, scriviamo direttamente i risultati:

$\begin{displaymath} \omega = \frac{2m'v\Delta}{m'\Delta^2+I} \quad\quad v' = v \frac{m'\Delta^2-I}{m'\Delta^2+I} \end{displaymath}$

Ora, in modo esatto, determiniamo di quanto si alza il centro della sbarra (che ora coincide con il suo centro di massa) scrivendo una conservazione dell'energia per la sola sbarra:

$\begin{displaymath} mg\delta = \frac{1}{2}I\omega^2 = 2\frac{md^2}{3} \left(\frac{m'v\Delta}{m'\Delta^2+I}\right)^2 \end{displaymath}$

Infine procediamo a semplificare anche questa formula, trascurando nel denominatore dell'ultima frazione il termine $m'\Delta^2$ rispetto a (poichè è proporzionale ad ). L'espressione per $\delta$ si semplifica allora in:

$\begin{displaymath} \delta = \frac{6v^2\Delta^2m'^2}{gd^2m^2} \sim 17\textrm{cm} \end{displaymath}$