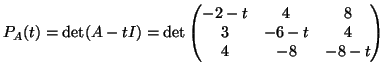
(1). Il polinomio caratteristico è dato da:
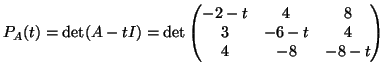
Riducendo a scala le matrici ![]() e
e ![]() si ottiene che
si ottiene che
![]() e
e
![]() quindi
quindi
![]() e
e
![]()
(4). La matrice ![]() non è diagonalizzabile. Dato che la
somma delle dimensioni degli autospazi è
non è diagonalizzabile. Dato che la
somma delle dimensioni degli autospazi è ![]() che è diverso dalla dimensione
dello spazio ambiente (
che è diverso dalla dimensione
dello spazio ambiente (![]() ).
).
![]()
Soluzione dell'esercizio 2 (1). Una ridotta a gradini di ![]() è data da
è data da
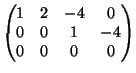
(2).
![]() e una base di
e una base di
![]() è data dalle colonne della
matrice
è data dalle colonne della
matrice ![]() corrispondenti alle colonne dei pivot, quindi una base di
corrispondenti alle colonne dei pivot, quindi una base di
![]() è data da
è data da
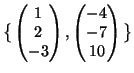 .
.
![]() . Per determinare una base del
nucleo risolviamo il sistema lineare omogeneo associato alla matrice
. Per determinare una base del
nucleo risolviamo il sistema lineare omogeneo associato alla matrice ![]() che è
equivalente a quello associato alla sua ridotta a scala:
che è
equivalente a quello associato alla sua ridotta a scala:
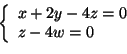 |
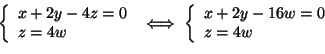 |
||
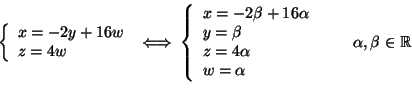 |
|||
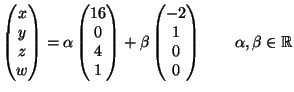 |
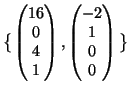 .
(3).
Riducendo a scala la matrice completa del sistema,
.
(3).
Riducendo a scala la matrice completa del sistema, 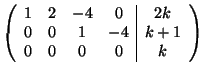
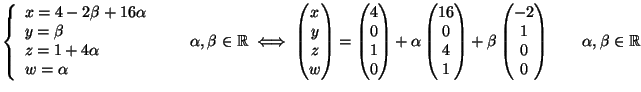
Soluzione dell'esercizio 3 (1). Applichiamo il processo di ortonormalizzazione di Gram-Schmidt ai due
vettori ![]() e
e ![]() .
.
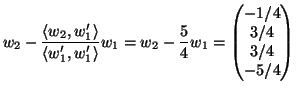 |
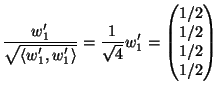 |
|||
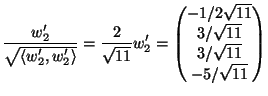 |
(2).
![]() è l'insieme dei vettori ortogonali ha tutti i vettori di
è l'insieme dei vettori ortogonali ha tutti i vettori di ![]() , quindi
, quindi
![]() se e solo se
se e solo se
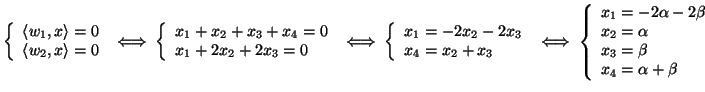
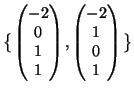 .
.
(3).
Dato che
![]() , allora necessariamente
, allora necessariamente ![]() e
e ![]() .
.
![]()
Soluzione dell'esercizio 4 (1). Scriviamo equazioni parametriche per ![]() .
.
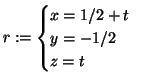
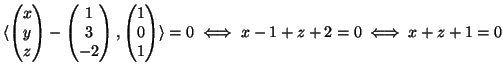
(2).
La retta cercata passa per ![]() ed ha direzione ortogonale a
ed ha direzione ortogonale a ![]() , ossia
parallela a
, ossia
parallela a ![]() , quindi ha equazioni parametriche
, quindi ha equazioni parametriche
(3).
Dato che le rette ![]() e
e ![]() sono entrambe ortogonali al piano
sono entrambe ortogonali al piano ![]() , sono tra
loro parallele, quindi un piano che le contiene esiste.
, sono tra
loro parallele, quindi un piano che le contiene esiste.
L'equazione del generico piano passante per ![]() è data da
è data da