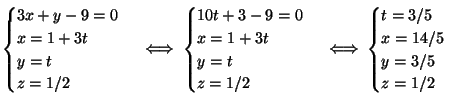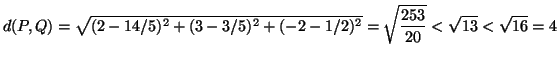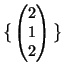 .
Una base di
.
Una base di 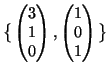 .
(4).
La matrice è diagonalizzabile, dato che la somma delle dimensioni degli
autospazi è
.
(4).
La matrice è diagonalizzabile, dato che la somma delle dimensioni degli
autospazi è
(1).
![]() .
(2).
Autovalori 0 e
.
(2).
Autovalori 0 e ![]() .
(3).
Una base di
.
(3).
Una base di ![]() è
è
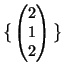 .
Una base di
.
Una base di ![]() è
è
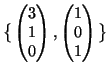 .
(4).
La matrice è diagonalizzabile, dato che la somma delle dimensioni degli
autospazi è
.
(4).
La matrice è diagonalizzabile, dato che la somma delle dimensioni degli
autospazi è ![]() che è pari alla dimensione dello spazio ambiente.
che è pari alla dimensione dello spazio ambiente.
![]()
Soluzione dell'esercizio 2 (1). Una ridotta a scala di ![]() è
è

(2). Una base di
![]() è data da
è data da
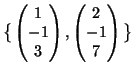 . Una base di
. Una base di ![]() è data da
è data da
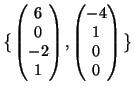 .
(3). Una ridotta a scala della matrice completa del sistema
.
(3). Una ridotta a scala della matrice completa del sistema
![]() è data da
è data da
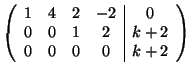
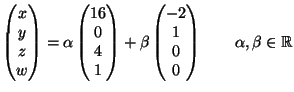
Soluzione dell'esercizio 3 (1). Base ortogonale
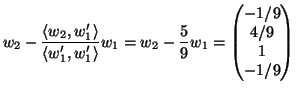 |
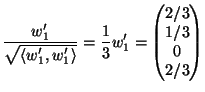 |
|||
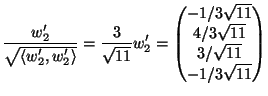 |
(2).
Una base di ![]() è data da
è data da
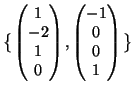
(3).
Osserviamo che
![]() , quindi
, quindi ![]() e
e ![]() .
.
![]()
Soluzione dell'esercizio 4 (1). Scriviamo equazioni parametriche per ![]() .
.
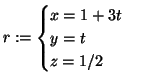
(2).
La retta ![]() ha equazioni parametriche
ha equazioni parametriche
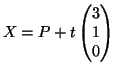
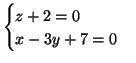
(3). La distanza di un punto di ![]() da un piano che
contiene
da un piano che
contiene ![]() sarà sicuramente inferiore della distanza tra le due rette
sarà sicuramente inferiore della distanza tra le due rette ![]() e
e
![]() . Calcoliamoci tale distanza. Per farlo calcoliamo il punto
. Calcoliamoci tale distanza. Per farlo calcoliamo il punto ![]() di
intersezione di
di
intersezione di ![]() con
con ![]() e quindi calcoliamo la distanza tra
e quindi calcoliamo la distanza tra ![]() e
e ![]() .
.
Calcolo di ![]() :
: