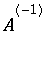e riducendo in forma di Gauss-Jordan la matrice ottenuta accostando la matrice
e la matrice identità, si ottiene la matrice costruita accostando l'identità con
. Verifichiamolo in un caso concreto
Esempio
Sappiamo che data una matrice invertibile
e riducendo in forma di Gauss-Jordan la matrice ottenuta accostando la matrice
e la matrice identità, si ottiene la matrice costruita accostando l'identità con
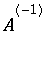. Verifichiamolo in un caso concreto
Prendiamo una matrice 5x5 a caso
> A:=randmatrix(5,5);
calcoliamone il determinante, per verificare che sia invertibile
> det(A);
costruiamo la matrice identità 5x5
>
delta := (i,j)->if i=j then 1 else 0 fi:
Id:=matrix(5,5,delta);
accostiamo le matrici. Questo può essere fatto usando l'istruzione concat
> C:=concat(A,Id);
eseguiamo la riduzione in forma di Gauss-Jordan
> CC:=gaussjord(C);
estraiamo la parte destra della matrice usando l'istruzione submatrix
> B := submatrix(CC,1..5,6..10);
Verifichiamo infine che la matrice
così ottenuta è effettivamente l'inversa di
> equal(B,inverse(A));
>
evalm(B &* A );
evalm(A &* B );
>