Soluzioni proposte

Soluzione dell'esercizio 1  Osserviamo che le tre rette L_i sono a due a due incidenti e i punti di intersezione sono dati da:

$$\begin{array}{rclcl} P_0 & = & (1,0) &&(L_2\cap L_3) \\ P_... ...(L_1\cap L_3) \\ P_2 & = & (1,1) &&(L_1\cap L_2) \end{array}$$

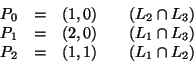
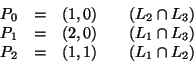
Le due rette M₁ e M₂ sono parallele, quindi non può esistere alcuna affinità che porti L₁ su M₁ e L₂ su M₂.

Le tre rette N_i sono anch'esse a due a due incidenti e i tre punti di intersezione sono:

$$\begin{array}{rclcl} Q_0 & = & (-3,0) &&(N_2\cap N_3) \\ Q... ...(N_1\cap N_3) \\ Q_2 & = & (0,1) &&(N_1\cap N_2) \end{array}$$

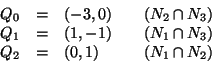
Sia i punti P₁ che i Q_i sono in posizione generica (non sono allineati) e quindi esiste una unica affinità $\varphi$ tale che $\varphi(P_i)=Q_i$ per ogni i. D'altra parte, visto che un'affinit'à porta rette in rette, tale affinità dovrà necessariamente portare ogni L_i su N_i (la retta per P_i e P_j viene portata sulla retta per Q_i e Q_j. D'altra parte, un'affinità che porti ogni retta L_i su Ni dovrà necessariamente portare i punti di intersezione delle rette L_i nei punti di intersezione delle corrispondenti rette N_i e quindi, per quanto detto sopra, una tale affinità è unica.

Costruiamola. Siano

$$\begin{array}{rcl} v_1 & = & P_1-P_0 = (1,0) \\ v_2 & = & ... ...& Q_1-Q_0 = (4,-1( \\ w_2 & = & Q_2-Q_0 = (-3,1) \end{array}$$

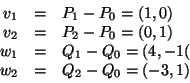
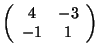L'applicazione lineare che porta v_i su w_i è allora definita dalla matrice $\left( \begin{array}{cc} 4 & -3 \\ -1 & 1 \end{array} \right)$e quindi l'affinità è del tipo:

$$\varphi(x_1,x_2)= \left( \begin{array}{cc} 4 & -3 \\ -1 ... ... + \left( \begin{array}{c} b_1 \\ b_2 \end{array} \right)$$

Per determinare b₁ e b₂ imponiamo che $\varphi(P_0)=Q_0$ e otteniamo:

$$\left( \begin{array}{c} b_1 \\ b_2 \end{array} \right) =... ..._0 = \left( \begin{array}{c} -7 \\ -1 \end{array} \right)$$

    

Soluzione dell'esercizio 2  Esplicitando il sistema rispetto alla variabile y si trova la seguente forma parametrica della retta r:

$$r=\{(3,0,-1)+t(-2,1,2):t\in\mathbb R\}$$

dato che i vettori direzione delle due rette sono linearmente indipendenti, non può esistere una retta che sia parallela ad entrambe.

Determiniamo una retta passante per P ed incidente ad entrambe. Osserviamo che se una tale retta esiste, deve essere contenuta nell'intersezione dei due piani $\Pi$, passante per P e contenente R, e $\Sigma$, passante per P e contenente s. Determiniamo questi due piani:

Il fascio di piani per r è dato da $\alpha(x + z - 2)+\beta(2 y - z - 1)=0$che contiene il punto P se e solo se $\beta = 0$ e quindi $\Pi$ ha equazione x+z-2=0.

Equazioni cartesiane della retta s sono date da:

$$\left\{ \begin{array}{l} x - z = 2 \\ 2 x - y = 1 \end{array} \right.$$

Quindi il fascio di piani per s è dato da: $\alpha(x - z - 2)+\beta(2 x - y - 1)=0$ che contiene il punto P se e solo se $-2\alpha - \beta =0$ e quindi il piano $\Sigma$ ha equazione 3 x - 2 y + z = 0.

L'intersezione dei due piani è data da:

$$\left\{ \begin{array}{l} x + z - 2 = 0 \\ 3 x - 2 y + z = 0 \end{array} \right.$$

Evidentemente questo sistema ha rango 2 e quindi descrive una retta R, quindi se una retta passante per P ed incidente alle due rette date esiste, allora deve coincidere con questaR. Proviamo che effettivamente R è incidente sia a r che a s.

Intersechiamo R con r:

$$\left\{ \begin{array}{l} x + z - 2 = 0 \\ 3 x - 2 y + z =... ...ay}{l} x = 1/3 \\ y = 4/3 \\ z = 5/3 \end{array} \right.$$

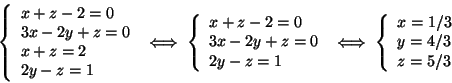
Intersechiamo R con s:

$$\left\{ \begin{array}{l} x + z - 2 = 0 \\ 3 x - 2 y + z =... ...} t = 1 \\ x = 2 \\ y = 3 \\ z = 0 \end{array} \right.$$

Per tantola retta R è effettivamnente incidente sia a r che a s.     

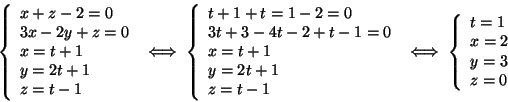
Soluzione dell'esercizio 3  Consideriamo le due coniche degeneri date dalle coppie di rette passanti rispettivamente per P₁P₃ e P₂P₄ e per P₁P₄ e P₂P₃, che hanno equazione rispettivamente:

$$x ( x - y - 1 ) = 0 \quad\hbox{\rm {e}}\quad y ( y - 2 ) = 0$$

Il fascio di coniche ha allora equazione:

$$\alpha x ( x - y - 1 ) + \beta y ( y - 2 ) = 0.$$

Perché il punto P₅ appartenga alla conica deve aversi $-\alpha - \beta = 0$, quindi la conica cercata, che è unica, ha equazione:

x² - y² - x y - x + 2 y = 0.

La matrice della conica è data da:

$$A= \left( \begin{array}{cc\vert c} 1 & -1/2 & -1/2 \\ -1/... ...-1 & 1 \\ \noalign{\hrule } -1/2 & 1 & 0 \end{array} \right)$$

Un semplice calcolo mostra che $\det A= -1/4 \ne 0$, per cui la conica è non degenede, e $\det A_infty = -5/4< 0$ e quindi la conica è un'iperbole.     

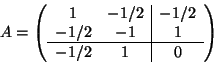
Soluzione dell'esercizio 4  Usiamo il metodo di Jacobi. Consideriamo la base standard dei polinomi, E₁=1,E₂=x,E₃=x², rispetto a tale base la matrice del prodotto scalare è data da:

$$\left( \begin{array}{ccc} 1 & 4 & 0 \\ 4 & 0 & 4 \\ 0 & 4 & 0 \end{array} \right)$$

. Dato che $\langle E_1,E_1\rangle=1$ possiamo considerare la nuova base:

$$\begin{array}{rcl} P_1 & = & E_1 \\ P_2 & = & E_2 - \frac{... ...1\rangle}{\langle E_1,E_1\rangle} E_1 = E_3 = x^2 \end{array}$$

Rispetto a questa nuova base la matrice del prodotto scalare diventa:

$$\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & -16 & 4 \\ 0 & 4 & 0 \end{array} \right)$$

Poniamo ora

$$\begin{array}{rcl} Q_1 & = & P_1 = 1 \\ Q_2 & = & P_2 = x ... ... = P_3 - \frac{1}{4} P_2 = x^2 - \frac{1}{4} x + 1 \end{array}$$

e otteniamo in tal modo una base ortogonale. La matrice rispetto a tale base è data da:

$$\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & -16 & 0 \\ 0 & 0 & -3 \end{array} \right)$$

quindi l'indice di positività è 1 e quello di negatività è 2.     

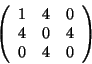
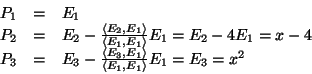
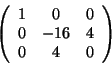
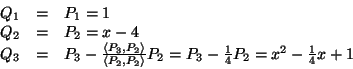
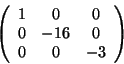
Soluzione dell'esercizio 5  1. Se $f\in V^*$ allora

$$\langle f,f\rangle=\sum_{i=1}^k f(v_i)^2 \ge 0.$$

qyuindi $\langle ,\rangle$ è semidefinito positivo.

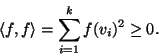
2. Indichiamo con $W=\left\langle {}v_1,\dots,v_k\right\rangle$. Chiaramente se $\ker f\supseteq W$ allora f(v_i)=0 per ogni i e quindi, per ogni $g\in V^*$si ha

$$\langle f,g\rangle=\sum_{i=1}^k f(v_i)g(v_i)=\sum_{i=1}^k 0g(v_i)=0.$$

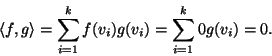
Viceversa, supponiamo che $\langle f,g\rangle=0$ per ogni g. Dimostriamolo prima per il caso in cui i v_i siano linearmente indipendenti. Se i v_i sono indipendenti, allora per ogni j esiste un funzionale $g_j\in V^*$ tale che

$$g_j(v_i)= \Big\langle \begin{array}{lcl} 0 &&\hbox{\rm {se }} i \ne j \\ 1 &&\hbox{\rm {se }} i = j \end{array}$$

(ad esempio si estenda $\{v_1,\dots,v_k\}$ ad una base di V e se ne prenda la base duale. Ma allora

$$0 = \langle f,g_j\rangle=\sum_{i=1}^k f(v_i)g_j(v_i)=f(v_j) \qquad \forall j=1,\dots,k$$

e quindi $\ker f\supseteq W$.

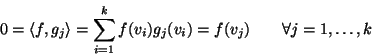
Vediamo ora il caso generale. Estraiamo da $\{v_1,\dots,v_k\}$ una base di W. Possima supporre, a meno di rinumerare i vettori, che i primi s dei v_icostituiscano una tale base. Ogni altro dei v_i si scriverà come combinazione lineare di questi, ossia:

$$v_{s+i} =\sum_{h=1}^s \alpha_{ih}v_h\qquad i=1,\dots,k-s.$$

Siano $g_j\in V^*$ definiti come prima, rispetto a $v_1,\dots,v_s$, allora per ogni $j=1,\dots,s$ si ha:

$$\begin{array}{rcl} 0 & = & \displaystyle\langle f,g_j\rangle... ...{k-s} (\sum_{h=1}^s \alpha_{ih}f(v_h))\alpha_{ij} \end{array}$$

Detti $A=(\alpha_{ij})$ e $w=\in\mathbb R^{s}$ il vettore la cui j-esima componente è f(v_j), allora la relazione appena ottenuta si può riscrivere

$$0 = w + {}^t\!\!AAw$$

da cui, moltiplicando scalarmente per w (rispetto al prodotto scalare standard di $\mathbb R^s$), segue che

$$0 = w\cdot w + w\cdot {}^t\!\!AAw = w\cdot w + (Aw)\cdot(Aw).$$

Poiché i due addendi sono non negativi, affinché la loro somma sia nulla devono entrambi essere nulli. In particolare $w\cdot w=0$ e quindi w=0. Ma ciò significa che f(v_j)=0 per ogni $j=1,\dots,s$. Dato che i $v_1,\dots,v_s$ sono una base di W questo significa che $\ker f\supseteq W$.

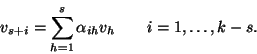
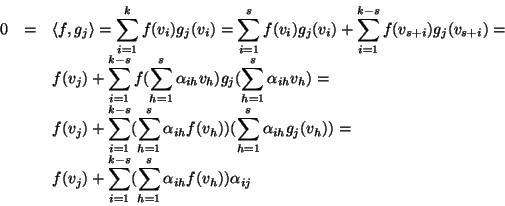
3. Osserviamo che:

$$\langle f,f\rangle=0\iff \sum_{i=1}^k f(v_i)^2 = 0 \iff f(v_i)=0\quad\forall i=1,\dots,k$$

e quindi, se $\{v_1,\dots,v_k\}$ è un sistema di generatori di V, ciò implica che f(v)=0 per ogni $v\in V$ e quindi f=0.

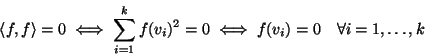
Viceversa, supponiamo che $\langle ,\rangle$ sia definito positivo ma che $\{v_1,\dots,v_k\}$ non sia un sistema di generatori di V. Detto $W=\left\langle {}v_1,\dots,v_k\right\rangle$, esisterebbe allora un funzionale non nullo tale che $\setbox \restrictbox=\hbox{$\hbox{$f$ }_{W}$ } \setbox 0\hbox{$f$ } {{f}\,\vrul... ...box depth\dp\restrictbox\, \hbox{\vrule depth\dp0 height \ht0 width0pt}_{W}}=0$, ma allora $\langle f,f\rangle=0$, contro l'assunto che $\langle ,\rangle$ sia definito positivo.