Oscillazioni complesse e fasori

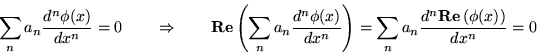
Molte equazioni della fisica sono equazioni differenziali lineari a coefficienti reali. Le soluzioni ``fisiche'', ovvero quelle che misuriamo effettivamente in un esperimento, corrispondono alle soluzioni reali (funzioni a valori reali) di queste equazioni. Ciononostante, è spesso più agevole studiare l'insieme delle soluzioni complesse (funzioni a valori complessi). È immediato mostrare che se una funzione complessa è soluzione di una equazione lineare a coefficienti reali, allora le sue parti reale ed immaginaria sono separatamente soluzioni (stavolta a valori reali) della stessa equazione. Per esempio, per la parte reale:

$$\sum_n a_n \frac{d^n\phi(x)}{dx^n} = 0 \ensuremath{\quad\... ...d^n\ensuremath{\mathbf{Re}}\left( {\phi(x)} \right)}{dx^n} = 0$$

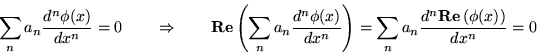
Un metodo per risolvere queste equazioni consiste quindi nel trovare una soluzione complessa dell'equazione tale che la sua parte reale al tempo zero corrisponda alle condizioni iniziali del problema. A causa della linearità, la parte reale della soluzione complessa sarà allora una soluzione del nostro problema con quelle condizioni iniziali.

Questa corrispondenza funziona fino a che non consideriamo trasformazioni non lineari su queste soluzioni; per esempio, fino a quando non vogliamo calcolare il quadrato di una soluzione (come avviene per una potenza assorbita o per un flusso di energia). Infatti la parte reale del prodotto di due numeri complessi non coincide con il prodotto delle parti reali dei due numeri complessi:

$$z_1 = a+ib \quad\quad z_2 = c+id \quad\quad \textrm{ma} \q... ...{z_1} \right)\ensuremath{\mathbf{Re}}\left( {z_2} \right) = ac$$

Passiamo ora al cosidetto metodo dei fasori. Questo è un metodo geometrico che consente la manipolazione di due o più oscillazioni armoniche della stessa frequenza. Un fasore $\vec{P}$ è un vettore applicato nell'origine. Se $\vec{P}$ compie un moto circolare uniforme, la sua proiezione sull'asse $\hat{x}$, $x_P(t)$, è soggetta ad un moto oscillatorio armonico; se poniamo $R=\vert\vec{P}\vert$ la sua coordinata è infatti; $$x_P(t) = R\cos(\omega t + \alpha)$$

Un'oscillazione armonica si può dunque sempre interpretare come la proiezione di un moto circolare. L'utilità del concetto di fasore è evidente quando si vogliono confrontare le fasi di oscillazione armonica di uguale frequenza. Confrontiamo per esempio $x_P$ con $\dot{x}_P$ e $\ddot{x}_P$:

$$\begin{eqnarray*} x_P & = & R\cos(\omega t + \alpha) \\ \dot{x}_P & = & -\ome... ...a) = \omega^2 R \cos\left([\omega t + \alpha] + \pi \right) \\ \end{eqnarray*}$$

Tutte e tre le funzioni sono oscillazioni armoniche, con diversa ampiezza e fase. Osserviamo che $\dot{x}_P$ è in anticipo di fase di $\frac{\pi}{2}$ rispetto a $x_P$; $\ddot{x}_P$ è in anticipo di fase di $\frac{\pi}{2}$ rispetto a $\dot{x}_P$ e di $\pi$ rispetto a $x_P$. Se esprimiamo queste oscillazioni mediante i fasori $\vec{P}$, $\vec{P'}$ e $\vec{P''}$ aventi moduli rispettivamente $R$, $\omega R$ ed $\omega^2 R$, abbiamo lo schema rappresentato in figura. La terna $\vec{P}$, $\vec{P'}$ e $\vec{P''}$ ruota con velocità $\vec{\omega}$ costante; in figura è rappresentata la situazione all'istante $t=0$.

Consideriamo per esempio due punti, $P$ e $Q$, che ruotano con velocità angolare costante su di una traiettoria circolare di raggio $R$; $P$ sia in anticipo rispetto a $Q$. Le proiezioni di $P$ e di $Q$ sull'asse delle $x$, cioè i punti $x_P$ ed $x_Q$, si muovono sull'asse $x$ di moto oscillatorio:

$$x_P = R\cos(\omega t) \ensuremath{\quad\quad \textrm{e} \quad\quad} x_Q = R\cos(\omega t - \alpha)$$

La rappresentazione di $x_P$ e $x_Q$ mediante fasori vede i vettori $\vec{P}$ e $\vec{Q}$ ruotare con velocità angolare costante $\vec{\omega}$. Si dice che il vettore $\vec{P}$ è in anticipo di fase rispeto a $\vec{Q}$ di $\alpha$, o, in maniera equivalente, che $\vec{Q}$ è in ritardo di fase rispetto a $\vec{P}$ di $\alpha$. In generale, fasori che ruotano alla stessa velocità corrispondono ad oscillazioni con la stessa frequenza (e che quindi conservano la loro differenza di fase).