Next: Geometria 3 febbraio 2000.
Up: Esercizi
Previous: Geometria 9 luglio 1999
Indice
Rispondere, giustificando brevemente la risposta, ad almeno due delle
prime quattro domande e risolvere il maggior numero degli esercizi seguenti.
Domande.
- Siano
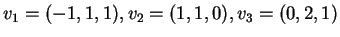 in
in 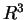 . Esiste una
applicazione
lineare
. Esiste una
applicazione
lineare
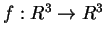 , tale che
, tale che
- Siano
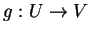 ed
ed
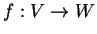 applicazioni lineari. È vero che
applicazioni lineari. È vero che
- Sia
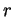 una retta in
una retta in 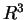 e
e 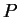 un punto fuori di essa. Sia
un punto fuori di essa. Sia
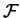 il fascio
di piani che contiene
il fascio
di piani che contiene 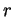 e
e
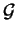 l'insieme dei
piani che contengono
l'insieme dei
piani che contengono 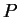 .
Esiste sempre un piano comune a
.
Esiste sempre un piano comune a
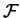 e
e
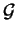 ?
?
- Sia
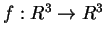 un'applicazione lineare tale che l'equazione
abbia infinite soluzioni.
La applicazione
un'applicazione lineare tale che l'equazione
abbia infinite soluzioni.
La applicazione 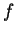 è suriettiva?
è suriettiva?
Esercizi.
1) Discutere e trovare le soluzioni del seguente sistema al variare del
parametro reale 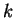 :
2) Discutere la diagonalizzabilità della seguente matrice
e trovare, se possibile, una base di autovettori.
:
2) Discutere la diagonalizzabilità della seguente matrice
e trovare, se possibile, una base di autovettori.
3) Siano 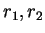 le rette in
le rette in 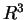 di equazione
di equazione
Trovare il piano parallelo a 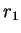 ed
ed 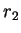 ed equidistante da
ed equidistante da 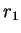 e
e 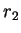 .
.
4) Dire per quali valori del parametro 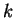 l'applicazione
l'applicazione
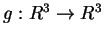 definita da
definita da
è lineare. Per tali valori scriverne la matrice rispetto alla base
canonica, determinare 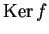 e scriverne una base.
e scriverne una base.
Soluzione
Domande
- La risposta è sì. Infatti esistono infinite applicazioni lineari con la
proprietà
richiesta. Tali applicazioni sono sono determinate dando l'immagine di un vettore
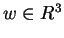 indipendente da
indipendente da 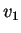 e
e 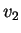 .
.
- La risposta è no. Infatti siano, per esempio,
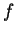 una applicazione non identicamente nulla e
una applicazione non identicamente nulla e 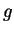 la
applicazione nulla. Allora
la
applicazione nulla. Allora
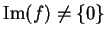 e
e
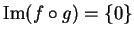
- La risposta è sì. Infatti esiste sempre un piano che contiene una retta e
passa per
un punto fuori di essa.
- La risposta è no. Infatti
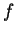 non è iniettiva.
non è iniettiva.
Esercizio 1.
La matrice dei coefficienti del sistema è la matrice:
Per calcolare il determinante della matrice 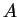 si può applicare lo sviluppo di Laplace
ad una
riga o una colonna della matrice oppure ridurla con il metodo di Gauss.
si può applicare lo sviluppo di Laplace
ad una
riga o una colonna della matrice oppure ridurla con il metodo di Gauss.
Una possibile riduzione è:
Il determinante di 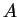 risulta:
Se
risulta:
Se
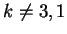 esiste una e una sola soluzione del sistema.
esiste una e una sola soluzione del sistema.
La soluzione è
Se  il sistema dato è equivalente al sistema:
che ammette infinite soluzioni:
il sistema dato è equivalente al sistema:
che ammette infinite soluzioni:
Infine se 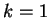 il sistema dato è equivalente al sistema:
che ammette infinite soluzioni:
il sistema dato è equivalente al sistema:
che ammette infinite soluzioni:
Esercizio 2.
Il polinomio caratteristico della matrice è :
dumque gli autovalori sono
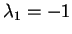 con molteplicità algebrica
con molteplicità algebrica 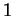 e
e
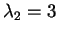 con molteplicità algebrica
con molteplicità algebrica 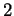 .
.
L'autospazio relativo all'autovalore 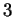 è
è
L'autospazio relativo all'autovalore 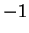 è
è
Concludiamo che la matrice è diagonalizzabile e una base di autovettori è data
Esercizio 3.
La retta 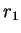 ha parametri direttori
ha parametri direttori 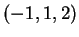 mentre la retta
mentre la retta 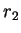 ha parametri direttori
ha parametri direttori
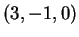 . Un generico piano
. Un generico piano 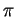 di equazione cartesiana
risulta parallelo alle rette
di equazione cartesiana
risulta parallelo alle rette 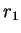 e
e 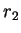 se e solo se il vettore
se e solo se il vettore
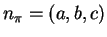 è
ortogonale ai vettori
è
ortogonale ai vettori
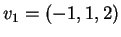 e
e
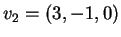 .
Devve essere allora verificato il sistema
da cui
L'equazione cartesiana di
.
Devve essere allora verificato il sistema
da cui
L'equazione cartesiana di 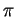 risulta allora essere
La distanza del piano
risulta allora essere
La distanza del piano 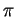 dalla retta
dalla retta 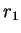 è
mentre la distanza del piano
è
mentre la distanza del piano 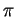 dalla retta
dalla retta 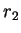 è
Imponendo che le distanze siano uguali si ottiene
pertanto l'equazione cartesiana di
è
Imponendo che le distanze siano uguali si ottiene
pertanto l'equazione cartesiana di 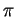 è:
è:
Esercizio 4.
L'applicazione è lineare solo per 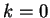 . In questo caso la matrice della applicazione è
. In questo caso la matrice della applicazione è
Poichè il determinante di 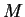 è non nullo abbiamo che il nucleo della applicazione è
costituito dal solo vettore nullo.
è non nullo abbiamo che il nucleo della applicazione è
costituito dal solo vettore nullo.




Next: Geometria 3 febbraio 2000.
Up: Esercizi
Previous: Geometria 9 luglio 1999
Indice
Andreatta Marco
2000-09-18
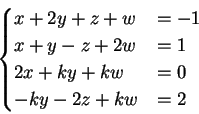
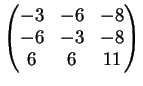
![]() le rette in
le rette in ![]() di equazione
di equazione
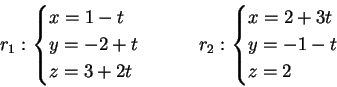
![]() l'applicazione
l'applicazione
![]() definita da
definita da
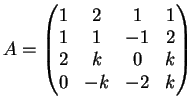
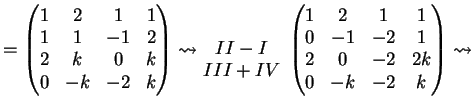
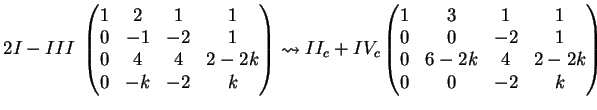
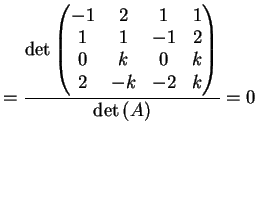
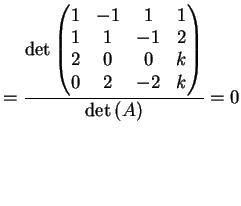
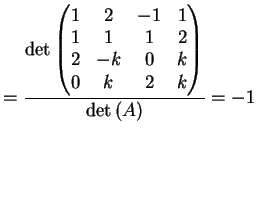
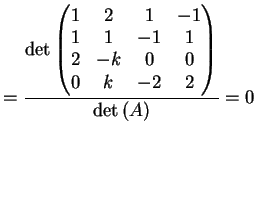
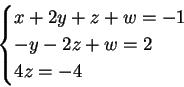
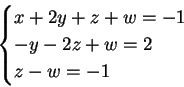
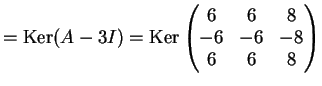
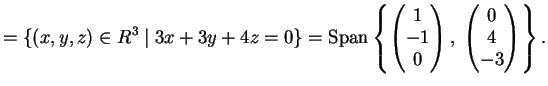
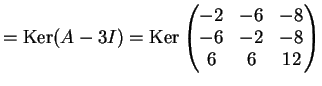
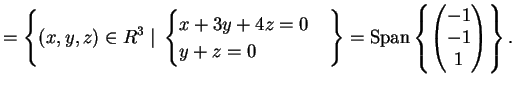
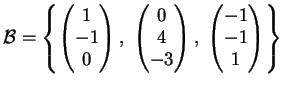
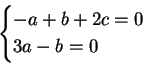
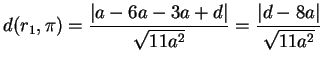
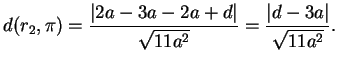
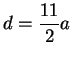
![]() . In questo caso la matrice della applicazione è
. In questo caso la matrice della applicazione è