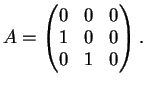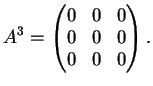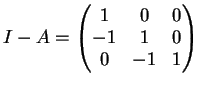Next: Geometria 12 luglio 2000
Up: Esercizi
Previous: Geometria 1 marzo 2000.
Indice
Domande.
- Siano
 ,
, 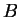 ,
, 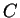 matrici
matrici
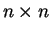 a coefficienti reali.
L'uguaglianza
implica
a coefficienti reali.
L'uguaglianza
implica
- Sia
 una matrice
una matrice
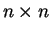 con
con
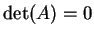 .
.
Il sistema
ammette
- Siano
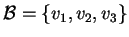 una base di
una base di 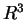 .
L'insieme:
.
L'insieme:
- Sia
 una matrice
una matrice
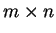 a coefficienti reali.
Le soluzioni del sistema lineare:
a coefficienti reali.
Le soluzioni del sistema lineare:
- Siano
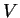 e
e 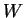 spazi vettoriali con
spazi vettoriali con 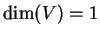 .
Sia
.
Sia
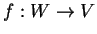 una applicazione lineare non nulla.
Allora
una applicazione lineare non nulla.
Allora
- Siano
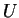 e
e 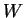 i sottospazi di
i sottospazi di 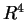 generati da:
La dimensione di
generati da:
La dimensione di 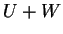 è :
è :
- Per quali valori del parametro reale
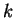 la matrice
è diagonalizzabile?
la matrice
è diagonalizzabile?
- Sia
 un endomorfismo di uno spazio vettoriale e sia
un endomorfismo di uno spazio vettoriale e sia 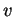 un autovettore relativo
all'autovalore
un autovettore relativo
all'autovalore 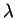 .
Il vettore
.
Il vettore
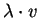 è un autovettore relativo all'autovalore:
è un autovettore relativo all'autovalore:
- Siano
 una retta parallela ad un piano
una retta parallela ad un piano 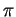 ed
ed  una retta incidente
il piano
una retta incidente
il piano 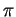 .
Le rette
.
Le rette  ed
ed  sono:
sono:
- Siano
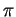 e
e 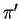 due piani paralleli e distinti.
Sia
due piani paralleli e distinti.
Sia 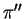 un piano
incidente
un piano
incidente 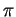 e
e 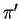 e siano
e siano
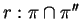 e
e
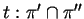 .
Le rette
.
Le rette
 e
e 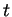 sono:
sono:
Esercizi.
1) Discutere e trovare le soluzioni del seguente sistema :
al variare del parametro reale 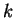 .
.
2) Sia  la matrice
la matrice
- Determinare autovalori e autospazi di
 .
.
- Se possibile determinare una base di autovettori di
 .
.
3) Sia  la retta passante per i punti
la retta passante per i punti 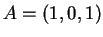 e
e
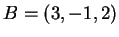 e sia
e sia 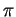 il piano ortogonale ad
il piano ortogonale ad  che passa per il punto
che passa per il punto  .
.
Sia  la retta di intersezione tra il piano
la retta di intersezione tra il piano 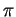 e il piano
e il piano 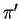 di
equazione
e sia
di
equazione
e sia 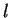 la retta parallela ad
la retta parallela ad  passante per il punto
passante per il punto 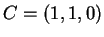 .
.
Si dica se le rette  ,
,  e
e 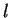 sono a due a due complanari, motivando la
risposta.
sono a due a due complanari, motivando la
risposta.
4) Sia
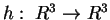 definita da
definita da
Provare che si tratta di una applicazione lineare e quindi scriverne la matrice
rispetto alla base canonica di 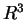 .
Calcolare
.
Calcolare
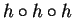 . Provare che l'applicazione
. Provare che l'applicazione
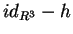 è invertibile.
è invertibile.
Soluzione
Esercizio 1.
La matrice completa associata al sistema è la matrice:
Una possibile riduzione a gradino per righe è la seguente:
Per
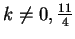 la matrice dei coefficienti del sistema ha rango
( massimo )
la matrice dei coefficienti del sistema ha rango
( massimo ) 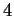 ,
sicchè si ha una sola soluzione:
,
sicchè si ha una sola soluzione:
Per 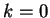 le matrici completa e incompleta del sistema hanno entrambe rango
le matrici completa e incompleta del sistema hanno entrambe rango 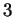 sichè abbiamo
infinite soluzioni, dipendenti da un parametro. Precisamente:
Infine per
sichè abbiamo
infinite soluzioni, dipendenti da un parametro. Precisamente:
Infine per
 non esistono soluzioni del sistema. Infatti la matrice
associata diventa :
L'equazione corrispondente alla terza riga è manifestamente falsa.
non esistono soluzioni del sistema. Infatti la matrice
associata diventa :
L'equazione corrispondente alla terza riga è manifestamente falsa.
Esercizio 2.
Il polinomio caratteristico della matrice è :
dunque gli autovalori sono 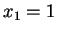 con molteplicità algebrica
con molteplicità algebrica 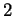 e
e
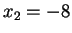 con molteplicità algebrica
con molteplicità algebrica  .
.
L'autospazio relativo all'autovalore  è
e risulta
Ne segue allora
Poiché
è
e risulta
Ne segue allora
Poiché
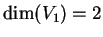 la matrice è diagonalizzabile.
la matrice è diagonalizzabile.
L'autospazio relativo all'autovalore 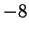 è
è
e si determina risolvendo il sistema
Risulta allora
Infine una base di autovettori di  è data dall'insieme:
è data dall'insieme:
Esercizio 3.
La retta  ha equazione
ha equazione
e il piano 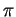 ha equazione
La retta
ha equazione
La retta  ha rappresentazione cartesiana
e rappresentazione parametrica
La retta
ha rappresentazione cartesiana
e rappresentazione parametrica
La retta 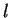 è pertanto:
Le rette
è pertanto:
Le rette 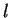 e
e  sono complanari perchè parallele.
sono complanari perchè parallele.
Le rette  ed
ed  sono ortogonali e quindi sono complanari
se e solo se si intersecano in un
punto, ovvero se e solo se
sono ortogonali e quindi sono complanari
se e solo se si intersecano in un
punto, ovvero se e solo se
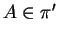 , ma questo non accade.
, ma questo non accade.
Le rette 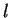 ed
ed  sono complanari se e solo se si intersecano in un punto, ma il sistema
formato dalle loro equazioni non ha soluzioni pertanto non sono complanari.
sono complanari se e solo se si intersecano in un punto, ma il sistema
formato dalle loro equazioni non ha soluzioni pertanto non sono complanari.
Esercizio 4.
Proviamo che sussistono le seguenti uguaglianze:
per ogni
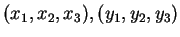 in
in 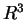 e per ogni
e per ogni 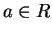 .
.
La prima uguaglianza è vera perchè
la seconda perchè
La matrice rispetto alla base canonica di 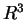 è:
La matrice di
è:
La matrice di
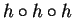 è
è 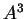 ed è, con facile calcolo,
L'applicazione (lineare !)
ed è, con facile calcolo,
L'applicazione (lineare !)
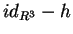 ha matrice
ha matrice 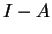 rispetto alla base canonica di
rispetto alla base canonica di 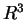 :
con
:
con
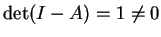 , da cui segue che
, da cui segue che
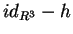 è invertibile.
è invertibile.




Next: Geometria 12 luglio 2000
Up: Esercizi
Previous: Geometria 1 marzo 2000.
Indice
Andreatta Marco
2000-09-18
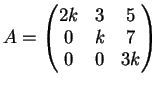
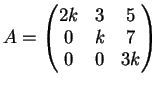
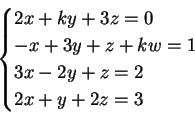
![]() la matrice
la matrice
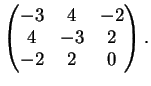
![]() definita da
definita da
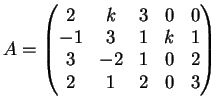
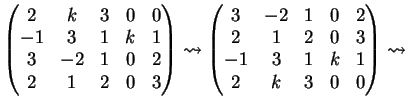
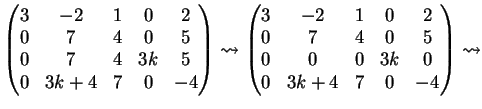
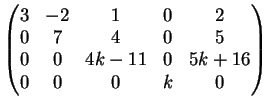
![]() la matrice dei coefficienti del sistema ha rango
( massimo )
la matrice dei coefficienti del sistema ha rango
( massimo ) ![]() ,
sicchè si ha una sola soluzione:
,
sicchè si ha una sola soluzione:
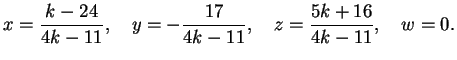
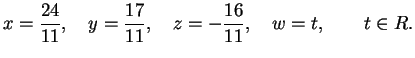
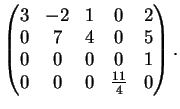
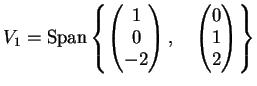
![]() è
è
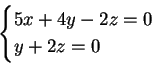
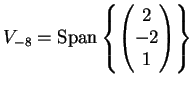
![]() ha equazione
ha equazione
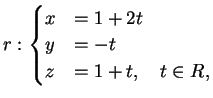
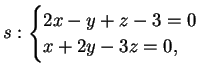
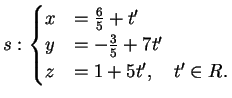
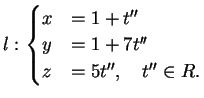
![]() ed
ed ![]() sono ortogonali e quindi sono complanari
se e solo se si intersecano in un
punto, ovvero se e solo se
sono ortogonali e quindi sono complanari
se e solo se si intersecano in un
punto, ovvero se e solo se
![]() , ma questo non accade.
, ma questo non accade.
![]() ed
ed ![]() sono complanari se e solo se si intersecano in un punto, ma il sistema
formato dalle loro equazioni non ha soluzioni pertanto non sono complanari.
sono complanari se e solo se si intersecano in un punto, ma il sistema
formato dalle loro equazioni non ha soluzioni pertanto non sono complanari.