Next: Geometria 20 giugno 2000.
Up: Esercizi
Previous: Geometria 3 febbraio 2000.
Indice
Domande.
- Sia
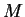 una matrice
una matrice
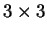 antisimmetrica, i. e.
antisimmetrica, i. e. 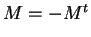 .
Allora:
.
Allora:
- Sia
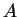 una matrice
una matrice
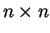 con
con
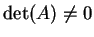 .
.
Il sistema
ammette
- Siano
 uno spazio vettoriale,
uno spazio vettoriale, 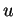 ,
, 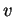 e
e 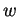 vettori di
vettori di  linearmente
dipendenti. I vettori
sono
linearmente
dipendenti. I vettori
sono
- Sia
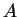 una matrice
una matrice
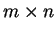 a coefficienti reali.
Le soluzioni del sistema lineare:
a coefficienti reali.
Le soluzioni del sistema lineare:
- Sia
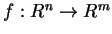 una applicazione lineare di matrice
una applicazione lineare di matrice 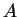 .
Se
.
Se 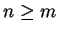 quali condizioni deve verificare
quali condizioni deve verificare 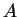 perché
perché 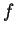 non sia
suriettiva?
non sia
suriettiva?
- Siano
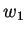 ,
,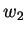 ,
, 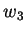 i vettori di
i vettori di  di coordinate:
Esistono applicazioni lineari
di coordinate:
Esistono applicazioni lineari
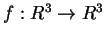 tali che
tali che
- La matrice
- Sia
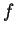 un endomorfismo di uno spazio vettoriale e sia
un endomorfismo di uno spazio vettoriale e sia 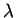 un
suo autovalore.
L'applicazione
un
suo autovalore.
L'applicazione 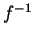 ammette come autovalore:
ammette come autovalore:
- Siano
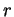 e
e 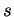 due rette parallele ad un piano
due rette parallele ad un piano 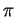 .
Le rette
.
Le rette 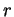 ed
ed 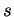 sono:
sono:
- Dati una retta
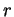 e un punto
e un punto 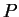 nello spazio, quante rette
esistono passanti per
nello spazio, quante rette
esistono passanti per 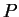 e ortogonali ad
e ortogonali ad 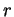 ?
?
Esercizi.
1) Discutere e trovare le soluzioni del seguente sistema :
al variare del parametro reale 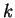 .
.
2) Sia 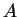 la matrice
la matrice
- Determinare autovalori e autospazi di
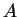 .
.
- Se possibile determinare una base di autovettori di
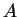 .
.
3) Sia 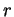 la retta di equazioni
e sia
la retta di equazioni
e sia 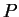 il punto
il punto 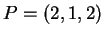 . Siano
. Siano 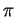 il piano contenente
il piano contenente 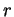 e passante
per
e passante
per 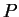 ,
, 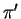 il piano contenente
il piano contenente 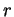 e ortogonale a
e ortogonale a 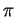 e
e 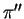 il piano
ortogonale ad
il piano
ortogonale ad 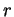 e passante per
e passante per 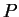 .
.
Detta 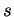 la retta di intersezione tra
la retta di intersezione tra 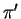 e
e 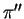 , determinare le
coordinate dei punti
, determinare le
coordinate dei punti 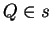 tali che
tali che
4) Sia
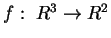 un'applicazione lineare.
Sapendo che
un'applicazione lineare.
Sapendo che
e che il nucleo di 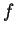 contiene, tra gli altri, i vettori
ricostruire
contiene, tra gli altri, i vettori
ricostruire 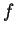 e scriverne la matrice rispetto alle basi canoniche di
e scriverne la matrice rispetto alle basi canoniche di
 e
e 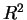 . Calcolare la dimensione del nucleo di
. Calcolare la dimensione del nucleo di 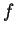 .
.
Soluzione
Esercizio 1.
La matrice associata al sistema è la matrice:
Una possibile riduzione a gradino, per righe, è
Per 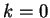 non esistono soluzioni del sistema. Infatti la matrice
associata al sistema diventa
L'ultima riga corrisponde all'equazione
non esistono soluzioni del sistema. Infatti la matrice
associata al sistema diventa
L'ultima riga corrisponde all'equazione 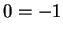 manifestamente falsa.
manifestamente falsa.
Per 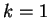 la matrice
associata al sistema diventa
la matrice
associata al sistema diventa
La matrice completa e la matrice incompleta hanno entrambe rango 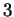 pertanto il sistema
ammette infinite soluzioni date da:
pertanto il sistema
ammette infinite soluzioni date da:
Se
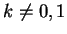 la matrice completa e la matrice incompleta hanno
entrambe rango
la matrice completa e la matrice incompleta hanno
entrambe rango 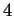 pertanto esiste una e una sola soluzione del sistema.
pertanto esiste una e una sola soluzione del sistema.
La soluzione è
Esercizio 2.
Il polinomio caratteristico della matrice è :
dunque gli autovalori sono
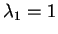 con molteplicità algebrica
con molteplicità algebrica 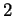 e
e
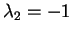 con molteplicità algebrica
con molteplicità algebrica 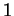 .
.
L'autospazio relativo all'autovalore 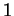 è
è
e risulta
Ne segue allora
Poiché
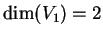 la matrice è diagonalizzabile.
la matrice è diagonalizzabile.
L'autospazio relativo all'autovalore 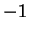 è
e si determina risolvendo il sistema
La matrice completa associata a questo sistema è:
Una possibile riduzione a gradino, per righe, è
Il sistema associato all'ultima matrice è il sistema:
pertanto
Infine una base di autovettori di
è
e si determina risolvendo il sistema
La matrice completa associata a questo sistema è:
Una possibile riduzione a gradino, per righe, è
Il sistema associato all'ultima matrice è il sistema:
pertanto
Infine una base di autovettori di 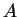 è data dall'insieme:
è data dall'insieme:
Esercizio 3.
Il fascio di piani per 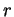 ha equazione:
ha equazione:
ossia
Per trovare 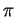 imponiamo il passaggio per
imponiamo il passaggio per 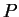 e otteniamo:
Per trovare
e otteniamo:
Per trovare 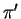 imponiamo che il vettore normale al piano sia ortogonale al vettore normale a
imponiamo che il vettore normale al piano sia ortogonale al vettore normale a
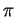 . Quest'ultimo ha coordinate
. Quest'ultimo ha coordinate 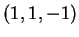 , pertanto imponiamo:
L'equazione di
, pertanto imponiamo:
L'equazione di 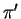 è :
Il piano
è :
Il piano 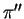 ha come vettore normale il vettore direzione di
ha come vettore normale il vettore direzione di 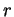 , che è
, che è 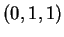 , e passa
per
, e passa
per 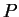 , dunque:
La retta
, dunque:
La retta 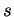 ha equazione cartesiana:
e equazioni parametriche:
I punti
ha equazione cartesiana:
e equazioni parametriche:
I punti 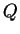 avranno quindi coordinate
avranno quindi coordinate
Ora:
e
I punti cercati sono quelli per i quali:
ovvero
Otteniamo quindi i punti:
Esercizio 4.
I tre vettori
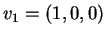 ,
,
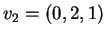 e
e
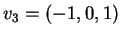 sono linearmente
indipendenti e quindi formano una base di
sono linearmente
indipendenti e quindi formano una base di  . Risulta infatti
. Risulta infatti
Le posizioni
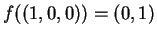 e
e
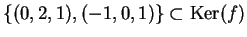 individuano l'applicazione lineare
individuano l'applicazione lineare
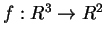 .
Evidentemente è
.
Evidentemente è
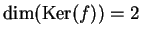 .
.
Procuriamoci ora 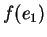 ,
, 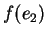 e
e 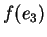 , essendo come al solito
, essendo come al solito
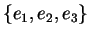 la base canonica di
la base canonica di  .
.
Come si può ricavare facilmente è 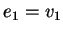 ,
,
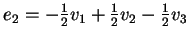 e
e
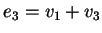 , pertanto
, pertanto
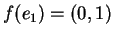 ,
,
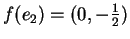 ,
,
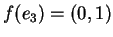 .
.
La matrice richiesta è:




Next: Geometria 20 giugno 2000.
Up: Esercizi
Previous: Geometria 3 febbraio 2000.
Indice
Andreatta Marco
2000-09-18
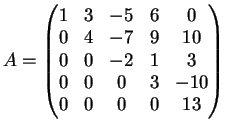
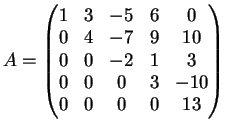
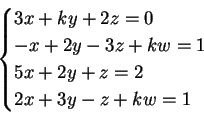
![]() la matrice
la matrice
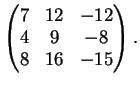
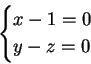
![]() la retta di intersezione tra
la retta di intersezione tra ![]() e
e ![]() , determinare le
coordinate dei punti
, determinare le
coordinate dei punti ![]() tali che
tali che
![]() un'applicazione lineare.
Sapendo che
un'applicazione lineare.
Sapendo che
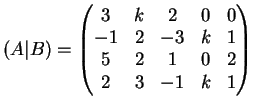
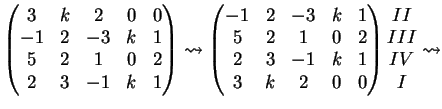
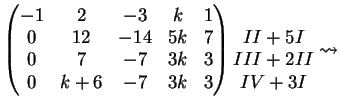
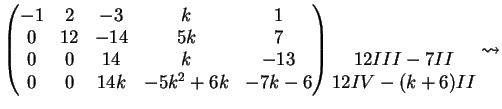
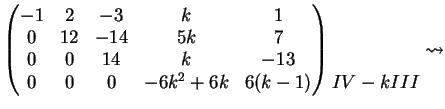
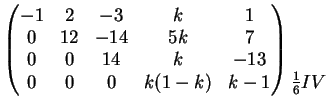
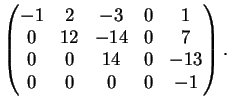
![]() la matrice
associata al sistema diventa
la matrice
associata al sistema diventa
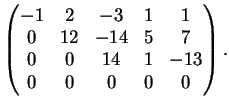
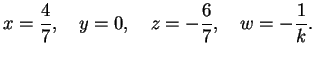
![]() con molteplicità algebrica
con molteplicità algebrica ![]() e
e
![]() con molteplicità algebrica
con molteplicità algebrica ![]() .
.
![]() è
è
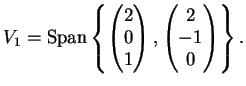
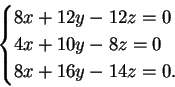
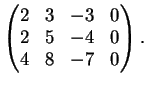
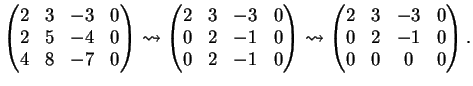
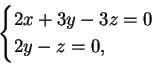

![]() ha equazione:
ha equazione:
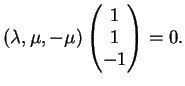
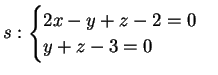
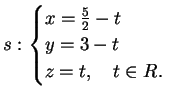
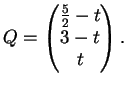
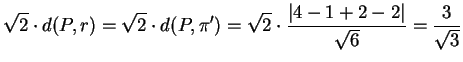
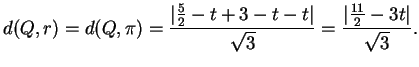
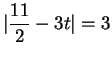
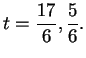
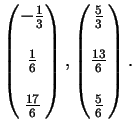
![]() ,
,
![]() e
e
![]() sono linearmente
indipendenti e quindi formano una base di
sono linearmente
indipendenti e quindi formano una base di ![]() . Risulta infatti
. Risulta infatti
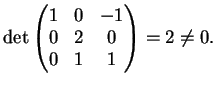
![]() ,
, ![]() e
e ![]() , essendo come al solito
, essendo come al solito
![]() la base canonica di
la base canonica di ![]() .
.
![]() ,
,
![]() e
e
![]() , pertanto
, pertanto
![]() ,
,
![]() ,
,
![]() .
.