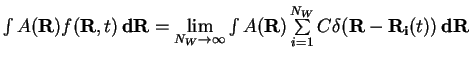- ... wavefunction3.1
- One of the reasons for using the product of
wavefunctions as the probability distribution instead of sampling
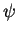 is that the average over the latter is ill defined
is that the average over the latter is ill defined
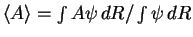 , on the contrary the
average over the product of wavefunctions has the meaning of the
mixed estimator
, on the contrary the
average over the product of wavefunctions has the meaning of the
mixed estimator
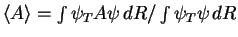
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... distribution3.1
-
The formula (3.26) should be understood in the statistical sense,
the average of any value
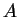 over the l.h.s.and r.h.s distributions
are equal to each other in the limit when size of the population
over the l.h.s.and r.h.s distributions
are equal to each other in the limit when size of the population
 tends to infinity
tends to infinity
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... energy3.1
- In real DMC
simulations the upper limit of the integrals is truncated by
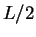 .
The ``tail'' energy, which is small and is typically much less than
.
The ``tail'' energy, which is small and is typically much less than
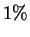 of the total energy can be approximated by the formula
of the total energy can be approximated by the formula
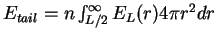 . The idea is
that at large distances, where the integral is evaluated, one can
safely assume uniform distribution of particles.
. The idea is
that at large distances, where the integral is evaluated, one can
safely assume uniform distribution of particles.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 3.1
3.1
-
It is necessary to note that here the ``diffusion'' occurs in
imaginary time and it has nothing to do with diffusion in real space.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... general4.1
- The only
exception[11] known to us takes place in the vicinity
of the
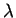 -transition in liquid
-transition in liquid 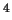 He, where
He, where
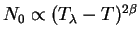 while
while
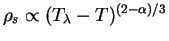 ,
and
,
and
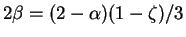 with
with 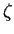 positive.
Still, for
positive.
Still, for 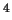 He both indices
He both indices 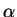 and
and
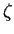 are very small, so with very good accuracy
are very small, so with very good accuracy
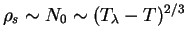 and the difference is so small that
there is no hope to measure it experimentally.
and the difference is so small that
there is no hope to measure it experimentally.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... squared6.1
- The
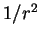 dependence can
be calculated directly from (1.45) by taking the limit
dependence can
be calculated directly from (1.45) by taking the limit 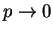 . Then
. Then 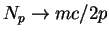 and integral (1.45) takes the form of
a Fourier transform of a Coulomb potential
and integral (1.45) takes the form of
a Fourier transform of a Coulomb potential
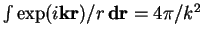 and produces the first term of eq.
(B.5).
and produces the first term of eq.
(B.5).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.