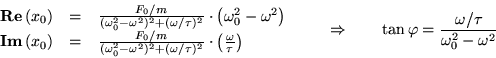| (1) |
L'equazione di un oscillatore armonico forzato e smorzato è:
dove tutti i parametri sono numeri reali.
Il modo più conveniente per risolverla consiste nell'immaginare
una eccitazione di tipo complesso
![]() al posto dell'eccitazione effettiva
al posto dell'eccitazione effettiva
![]() .
Osserviamo che essendo
.
Osserviamo che essendo
l'eccitazione effettiva ![]() coincide con la parte reale di
coincide con la parte reale di ![]() .
Poichè la soluzione dell'equazione differenziale (1)
con la parte non omogenea sarà una funzione complessa, di essa noi
considereremo solo la parte reale, cioè quella corrispondente
all'eccitazione effettiva:
.
Poichè la soluzione dell'equazione differenziale (1)
con la parte non omogenea sarà una funzione complessa, di essa noi
considereremo solo la parte reale, cioè quella corrispondente
all'eccitazione effettiva:
![]() . Dunque concentriamoci ora
sull'equazione:
. Dunque concentriamoci ora
sull'equazione:
È intuibile che per tempi grandi il sistema oscillerà con la
stessa frequenza della forza di eccitazione (soluzione asintotica),
mentre per tempi piccoli il moto è fortemente dipendente dalle
condizioni iniziali e la soluzione asintotica viene sommata a contributi
che decrescono esponenzialmente nel tempo (questa è la fase transiente,
vedere la sezione 1.3). Cerchiamo dunque una soluzione
della forma
![]() , con
, con ![]() un numero complesso
qualsiasi. Sostituendo
un numero complesso
qualsiasi. Sostituendo ![]() e le sue derivate nella precedente
equazione troviamo che:
e le sue derivate nella precedente
equazione troviamo che:
Dunque ![]() ha sicuramente una parte immaginaria. Risulta conveniente
esprimere
ha sicuramente una parte immaginaria. Risulta conveniente
esprimere ![]() in forma polare,
in forma polare,
![]() (ora
(ora ![]() è un
numero reale positivo). Allora la soluzione dell'equazione differenziale
diventa la seguente (di cui a noi interessa, come spiegato precedentemente,
solo la parte reale):
è un
numero reale positivo). Allora la soluzione dell'equazione differenziale
diventa la seguente (di cui a noi interessa, come spiegato precedentemente,
solo la parte reale):
Dobbiamo ora valutare l'ampiezza e la fase di questa oscillazione.
Cominciamo con il calcolare ![]() a partire dall'equazione
2:
a partire dall'equazione
2:
![]() è la fase del numero complesso
è la fase del numero complesso ![]() , quindi
, quindi
![]() :
:
e dunque: