Introduzione e richiami

Le funzioni di stato sono associate a quantità fisiche che hanno un valore individuato unicamente dallo stato termodinamico in cui un dato sistema si trova. Siccome spesso avremo a che fare con sistemi termodinamici a due gradi di libertà (ovvero sistemi in cui possiamo scegliere il valore di al più due variabili, mentre tutte le altre sono determinate dalle equazioni di stato), considereremo solo funzioni di stato a due variabili. Data una funzione $g$ dipendente dalle variabili $x$ ed $y$, una sua ``piccola variazione'' prende il nome di differenziale (talvolta chiamato differenziale esatto, ma il termine ``esatto'' è ovviamente ridondante):

$$dg = \ensuremath{\left( \ensuremath{\frac{\partial{g}}{\par... ... \ensuremath{\frac{\partial{g}}{\partial{y}}} \right)_{\!x}}dy$$

Siccome $g$ è una funzione di stato, un integrale di $dg$ dipende unicamente dagli estremi di integrazione, non dal particolare cammino $\gamma$ di integrazione scelto:

$$\int_{\gamma} dg = \int_{g_i}^{g_f} dg = g_f - g_i = \in... ... \ensuremath{\frac{\partial{g}}{\partial{y}}} \right)_{\!x}}dy$$

la catena di identità precedente è valida per qualunque cammino $\gamma$ che conduce dallo stato iniziale $i$ (dove $g$, $x$ ed $y$ assumono i valori $g_i$, $x_i$ e $y_i$) allo stato finale $f$ (dove $g$, $x$ ed $y$ assumono i valori $g_f$, $x_f$ e $y_f$).

Non tutte le ``piccole'' quantità termodinamiche sono comunque differenziali esatti. Le due più importanti che non rientrano in questa categoria sono il calore ed il lavoro. Nè il calore nè il lavoro sono funzioni di stato o, se vogliamo, nè gli scambi infinitesimi di lavoro nè quelli di calore sono differenziali di funzioni di stato termodinamico.

Ne segue che in generale i loro integrali dipendono non solo dagli stati iniziali e finali individuati da una certa trasformazione reversibile, ma dalla particolare trasformazione (curva termodinamica) $\gamma$. Per rimarcare questo fatto chiameremo uno scambio infinitesimo di lavoro $\lambda$ e non $dL$, poichè non esiste nessuna funzione di stato $L$. Allo stesso modo introdurremo il simbolo $\omega$ per uno scambio infinitesimo di calore, invece di $dQ$.

Le quantità infinitesime $\lambda$ ed $\omega$ sono ``forme differenziali'', ovvero funzioni integrabili lungo una curva termodinamica $\gamma$ (che corrisponde ad una certa trasformazione revesibile), tali che il loro integrale rappresenta lo scambio complessivo della quantità associata lungo la curva:

$$L(\gamma) = \int_{\gamma} \lambda \ensuremath{\quad\quad \textrm{e} \quad\quad} Q(\gamma) = \int_{\gamma} \omega$$

Per i sistemi termodinamici semplici che considereremo nel seguito, il lavoro è sempre una pressione moltiplicata per una variazione di volume, quindi in pratica $\lambda$ potrà sempre essere sostituito dalla quantità $-P dV$ (prendiamo il segno meno, intendendo $\lambda$ come il lavoro fatto dall'ambiente sul sistema, che è positivo quando il volume diminuisce). Con la stessa convenzione, $\omega$ sarà il calore che fluisce dall'ambiente al sistema.

Nonostante $\lambda$ ed $\omega$ non siano differenziali, la prima legge della termodinamica afferma che una loro particolare combinazione non dipende dalla trasformazione che il sistema subisce, a patto che questa sia reversibile. Questa combinazione è dunque un differenziale esatto; chiameremo il suo integrale energia interna del sistema:

$$dU = \omega + \lambda = \omega - P dV$$

Analogamente, il secondo principio della termodinamica per trasformazioni reversibili può pure essere espresso dicendo che, nonostante $\omega$ non sia un differenziale, il rapporto fra $\omega$ e la temperatura $T$ lo è. Si dice anche che $\frac{1}{T}$ è il fattore integrante di $\omega$. Chiameremo entropia la funzione di stato associata al differenziale che abbiamo trovato:

$$dS = \frac{\omega}{T}$$

Nel seguito faremo uso del fatto che le funzioni di stato termodinamico sono delle funzioni differenziabili. Ne segue che per le derivate seconde l'ordine di derivazione può essere invertito senza che il risultato cambi; questa proprietà puramente matematica prende il nome di relazione di Schwarzt:

$$\left[ \ensuremath{\ensuremath{\frac{\partial{}}{\partial{y... ...ensuremath{\frac{\partial{{}^2g}}{\partial{{x} \partial{y}}}}}$$

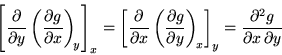
Prima di passare ad esaminare le proprietà delle principali funzioni di stato, ricordiamo l'equazione di stato dei gas reali, detta anche equazione di Van der Waals. In questa equazione il volume del gas è sostituito da una sorta di ``volume efficace'' pari alla differenza fra il volume $V$ del contenitore ed il volume proprio $b$ del gas. Inoltre, la ``pressione efficace'' è aumentata rispetto alla pressione propria di un termine $a/V^2$ che tiene conto degli urti fra le molecole del gas. Ovviamente, l'equazione di Van der Waals si riduce all'equazione di stato dei gas perfetti nel limite in cui i parametri $a$ e $b$ vanno a zero.

$$\left( P + \frac{a}{V^2} \right) \left( V - b \right) = nRT$$ (1)