Soluzioni di problemi vari

Esercizio 1
In assenza di qualsivoglia attrito, la biglia esercita solo una forza normale al blocco , bilanciata dal vincolo del piano di scorrimento, senza nemmeno rotolare. La dinamica dei due blocchi non ne è influenzata. La fune trasmette una forza fra i due blocchi, decelerando il blocco ed accelerando il blocco ; le equazioni del moto risultano:

$\begin{displaymath} \left\{ \begin{array}{lll} m_A a & = & F - T \\ m_B a & = & T \\ \end{array} \right. \end{displaymath}$

dove è l'accelerazione comune ai due blocchi (essi sono vincolati dalla fune a muoversi con la stessa legge del moto) e è il modulo della tensione della corda (si immagina che $\vec{F}$ e $\vec{T}$ giacciano entrambi nel piano orizzontale. Eliminando si calcola immediatamente l'accelerazione comune:

$\begin{displaymath} a = \frac{F}{m_A + m_B} \sim 8.57\textrm{m/s$^2$} \end{displaymath}$

e sostituendola nella seconda equazione si ricava :

$\begin{displaymath} T = m_B a = F \frac{m_B}{m_A + m_B} \sim 17.14\textrm{N} \end{displaymath}$

La biglia, che non si muove, cadrà dal bordo del blocco quando quest'ultimo si sarà mosso di cm dalla posizione iniziale, ovvero:

$\begin{displaymath} \frac{1}{2}at^2 = d \quad\quad \rightarrow \quad\quad t = \sqrt{\frac{2d}{a}} \sim 0.153\textrm{s} \end{displaymath}$

In caso di attrito poi ogni blocco viene decelerato da una forza proporzionale alla componente normale al piano di scorrimento del peso complessivo che giace sulla superficie di appoggio, ovvero il blocco viene decelerato $m_Ag\mu$ ed il blocco di $(m_B + m)g\mu$ . Inoltre l'attrito della pallina sul blocco decelera ulteriormente il blocco (ed accelera la pallina). Le equazioni del moto precedenti diventano:

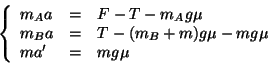
$\begin{displaymath} \left\{ \begin{array}{lll} m_A a & = & F - T - m_A g \mu \... ...mu - m g \mu \\ m a' & = & m g \mu \\ \end{array} \right. \end{displaymath}$

come prima eliminiamo :

$\begin{displaymath} T = F - m_A a - m_A g \mu \end{displaymath}$

sostituiamo nella seconda e ricaviamo :

$\begin{displaymath} m_B a = F - m_A a - g \mu ( m_A + m_B + 2m) \quad\quad \ri... ...mu ( m_A + m_B + 2 m )}{m_A + m_B} \sim 6.58\textrm{m/s$^2$} \end{displaymath}$

utilizzando ora ricaviamo il valore di :

$\begin{displaymath} T = F - m_A a - m_A g \mu \sim 17.28\textrm{N} \end{displaymath}$

Infine calcoliamo quando la pallina cade; nel riferimento accelerato del blocco la pallina sente una forza di attrito $ma'=mg\mu$ ed una forza apparente dovuta alla accelerazione del blocco sottostante pari a . La forza effettiva è dunque $ma - mg\mu$ , e la pallina cade quando la distanza percorsa è pari a :

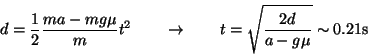
$\begin{displaymath} d = \frac{1}{2}\frac{ma - mg\mu}{m}t^2 \quad\quad \rightar... ...\quad\quad t = \sqrt{\frac{2d}{a-g\mu}} \sim 0.21\textrm{s} \end{displaymath}$

Esercizio 2
La velocità massima alla quale la curva puó essere percorsa è quella che richiede una accelerazione centripeta uguale al massimo attrito possibile. Naturalmente stiamo supponendo che il motore della macchina compensi l'attrito volvente nella direzione del moto della macchina.

$\begin{displaymath} \frac{mv^2}{R} = \mu m g \quad\quad \rightarrow \quad\quad ... ... \sqrt{R \mu g} \sim 18.53\textrm{m/s} \sim 66.7\textrm{km/h} \end{displaymath}$

Per il secondo caso, consideriamo un riferimento inerziale collegato alla strada. In questo riferimento le forze agenti sulla macchina sono il peso, la reazione vincolare normale e l'attrito. Definiamo una coppia di direzioni $\hat{z}$ ed $\hat{x}$ dirette verso l'alto e verso il centro della curva ortogonalmente a $\hat{z}$ , ed un'altra coppia $\hat{n}$ e $\hat{k}$ dirette lunga la normale uscente dalla strada e la parallela alla strada verso il centro della curva, tutte nel piano ortogonale alla macchina. Le espressioni delle forze e le condizioni affinchè il moto della macchina sia circolare uniforme con raggio in un piano orizzontale sono:

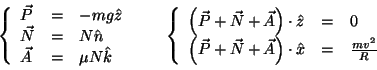
$\begin{displaymath} \left\{ \begin{array}{lll} \vec{P} & = & -mg\hat{z} \\ \... ...\cdot \hat{x} & = & \frac{mv^2}{R} \\ \end{array} \right. \end{displaymath}$

Con un primo passaggio ricaviamo il valore di :

$\begin{displaymath} N\left( \cos\alpha - \mu\sin\alpha \right) = mg \end{displaymath}$

Sostituendo l'espressione per nella seconda equazione otteniamo allora:

$\begin{displaymath} \frac{mg}{\cos\alpha - \mu\sin\alpha} \left( \sin\alpha + \mu\cos\alpha \right) = \frac{mv^2}{R} \end{displaymath}$

da cui si ricava facilmente la velocità:

$\begin{displaymath} v = \sqrt{gR}\sqrt{\frac{\tan\alpha + \mu}{1 - \mu\tan\alpha}} \sim 22.14\textrm{m/s} \sim 79.7\textrm{km/h} \end{displaymath}$

Come si vede il radicando nell'espressione di può diventare negativo per valori sufficientemente grandi di $\alpha$ (circa $55^\circ$ ); questo significa che per inclinazioni superiori a questo angolo di soglia la macchina non può in alcun caso scivolare verso l'esterno della pista.

Esercizio 3
Se il camion decelera con decelerazione , il tempo che ci mette a fermarsi sarà $t = \frac{v}{a}$ , ed in questo tempo percorrerà uno spazio pari a:

$\begin{displaymath} s = vt - \frac{1}{2}at^2 = \frac{v^2}{a} - \frac{v^2}{2a} = \frac{v^2}{2a} \end{displaymath}$

La cassa rimane solidale con il cassone se la decelerazione massima dovuta all'attrito statico, che vale $a'=g\mu$ , supera l'accelerazione . In questo caso il camion percorre:

$\begin{displaymath} s = \frac{v^2}{2a'} = \frac{v^2}{2g\mu} \sim 36.87\textrm{m} \end{displaymath}$

Se il camion sta procedendo in discesa, la reazione vincolare del cassone non è più ma $mg\cos\alpha$ . Inoltre la cassa è tirata verso il basso anche dalla componente della sua forza peso parallela al piano del cassone, ovvero $mg\sin\alpha$ . La forza di attrito massima effettiva (cioè comprensiva anche della componente del peso) risulta dunque $a'_d = g \left( \mu\cos\alpha - \sin\alpha \right)$ . Sostituendo nella relazione precedente otteniamo:

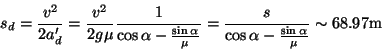
$\begin{displaymath} s_d = \frac{v^2}{2a'_d} = \frac{v^2}{2g\mu} \frac{1}{\cos\... ...s}{\cos\alpha - \frac{\sin\alpha}{\mu}} \sim 68.97\textrm{m} \end{displaymath}$

Infine nel caso della strada in salita la componente della forza peso parallela al piano del cassone ``aiuta'' l'attrito anzichè deprimerlo, per cui $a'_s = g \left( \mu\cos\alpha + \sin\alpha \right)$ e lo spazio diventa:

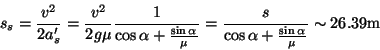
$\begin{displaymath} s_s = \frac{v^2}{2a'_s} = \frac{v^2}{2g\mu} \frac{1}{\cos\... ...s}{\cos\alpha + \frac{\sin\alpha}{\mu}} \sim 26.39\textrm{m} \end{displaymath}$

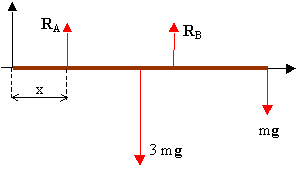
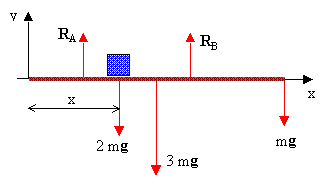
Esercizio 4
La corda in tensione esercita su ognuno dei due corpi una forza costante . Le accelerazioni (in modulo!) dei due corpi saranno allora legate dalla relazione:

$\begin{displaymath} F = m_1 a_1 = m_2 a_2 \quad\quad \rightarrow \quad\quad \frac{a_2}{a_1} = \frac{m_1}{m_2} \end{displaymath}$

Lo spazio percorso da entrambi i corpi si ricava con le usuali leggi del moto accelerato, e nel momento del contatto la somma degli spazi percorsi deve essere uguale alla distanza totale iniziale:

$\begin{displaymath} d_1 = \frac{1}{2}a_1 t^2 = d - d_2 = d - \frac{1}{2}a_2 t^2 \end{displaymath}$

utilizzando la relazione fra ed possiamo eliminare dall'ultimo membro:

$\begin{displaymath} d_1 = d - \frac{1}{2}a_1 t^2 \frac{a_2}{a_1} = d - \frac{1}{2}a_1 t^2 \frac{m_1}{m_2} \end{displaymath}$

ora notiamo che nell'ultimo membro troviamo di nuovo la espressione di per cui:

$\begin{displaymath} d_1 = d - d_1 \frac{m_1}{m_2} \quad\quad \rightarrow \quad\quad d_1 = \frac{d}{1 + \frac{m_1}{m_2}} \sim 10.82\textrm{m} \end{displaymath}$

Questo risultato in realtà non dipende dal fatto che la tensione della corda sia costante, ma solo dalla conservazione della quantità di moto. Infatti il sistema ragazza-slitta è inizialmente fermo, e siccome non interagisce con nient'altro (stiamo trascurando l'attrito con la superficie) la quantità di moto totale deve rimanere nulla. Questo impone una relazione fra i moduli delle velocità a tutti i tempi:

$\begin{displaymath} m_1 v_1(t) = m_2 v_2(t) \end{displaymath}$

Esprimendo le distanze percorse con relazioni integrali:

$\begin{displaymath} d = \int_0^T v_1(t)\;dt \quad + \quad \int_0^T v_2(t)\;dt \end{displaymath}$

possiamo ora sostituire con la relazione trovata dalla conservazione della quantità di moto:

$\begin{displaymath} d = \int_0^T v_1(t) \left( 1 + \frac{m_1}{m_2} \right)\;dt = \left( 1 + \frac{m_1}{m_2} \right) \int_0^T v_1(t) \;dt \end{displaymath}$

nell'ultimo integrale riconosciamo di nuovo l'espressione per e ci riconduciamo al risultato precedente:

$\begin{displaymath} d = \left( 1 + \frac{m_1}{m_2} \right) d_1 \quad\quad \rightarrow \quad\quad d_1 = \frac{d}{1 + \frac{m_1}{m_2}} \end{displaymath}$

Esercizio 5
a)

^Þ

Da queste due equazioni si ricava:

wpe2.gif (2454 byte)

^Þ

Esercizio 6
Per chiarezza ricordiamo che ``velocità'' nel testo dell'esercizio significa velocità nel riferimento non inerziale solidale con il disco rotante (nel riferimento inerziale bisogna aggiungere una componente azimutale di modulo $\omega\rho$ ). Utilizzeremo nel seguito un sistema di coordinate polari, dove $\ensuremath{\hat{e}_\rho}$ è il versore radiale (uscente) ed $\ensuremath{\hat{e}_\varphi}$ è il versore azimutale (che ``gira'' in senso antiorario).

Consideriamo le forze agenti nel riferimento non inerziale; oltre alla forza reale $-k\rho\,\ensuremath{\hat{e}_\rho}$ dovuta alla molla e quella dovuta alla reazione vincolare $F_v\ensuremath{\hat{e}_\varphi}$ , agiscono sulla biglia la forza centrifuga $m\rho\omega^2\ensuremath{\hat{e}_\rho}$ e la forza di Coriolis $F_C\ensuremath{\hat{e}_\varphi}$ . Il fatto che la forza di Coriolis sia puramente azimutale discende dal fatto che la biglia è obbligata a scorrere nella scanalatura, quindi la sua velocità $\dot{\rho}\ensuremath{\hat{e}_\rho}$ è puramente radiale. Di nuovo, siccome la biglia è obbligata a seguire la scanalatura, le forze agenti lungo $\ensuremath{\hat{e}_\varphi}$ si devono compensare esattamente, e possiamo considerare di avere un sistema equivalente ad uno inerziale, essenzialmente unidimensionale (lungo $\ensuremath{\hat{e}_\rho}$ ), in cui agisce una forza totale pari a $m(\omega^2 - \frac{k}{m})\rho\ensuremath{\hat{e}_\rho}$ . Il termine fra parentesi tonde ha le dimensioni di una pulsazione, ed è caratteristico del problema. Definiamo:

$\begin{displaymath} \Omega^2 = \frac{k}{m} - \omega^2 \end{displaymath}$

La risposta alla prima domanda è dunque semplice, la biglia rimane ferma nel riferimento rotante a distanza $\rho=d$ dal perno quando la forza totale ivi agente è nulla, cioè:

$\begin{displaymath} m(\omega^2 - \frac{k}{m})d = 0 \quad\quad \rightarrow \quad\quad \omega = \sqrt{\frac{k}{m}} \sim 86.6\textrm{rad/s} \end{displaymath}$

Questa condizione ovviamente significa $\Omega=0$ . È abbastanza intuitivo affermare che per velocità angolari minori la biglia sarà attirata dalla molla fino a sbattere contro l'asse di rotazione, per lo meno per continuità con il caso di velocità angolare nulla, e che per velocità angolari maggiori ci troveremo nell'altro regime dove la biglia ``scappa'' verso l'esterno del disco. Per calcolare la velocità finale $v_f = \dot{\rho}(t_f)$ , dobbiamo eguagliare l'energia potenziale della forza totale ( $\dot{\rho}$ è inizialmente nulla, quindi non c'e' energia cinetica) con l'energia finale:

$\begin{displaymath} \frac{1}{2}m\Omega^2d^2 = \frac{1}{2}mv_f^2 + \frac{1}{2}m\Omega^2\rho_f^2 \end{displaymath}$

Nel caso in cui $\rho(t_f)=\rho_f=0$ (biglia contro il perno) otteniamo:

$\begin{displaymath} \frac{1}{2}m\Omega^2d^2 = \frac{1}{2}mv_f^2 \quad\quad \rightarrow \quad\quad v_f = \Omega d \sim 17.7\textrm{m/s} \end{displaymath}$

Nel caso in cui $\rho(t_f)=\rho_f=R$ (biglia contro il bordo) abbiamo $\Omega^2<0$ ; facendo attenzione ai segni otteniamo:

$\begin{displaymath} \frac{1}{2}m\Omega^2d^2 - \frac{1}{2}m\Omega^2R^2 = \frac{... ...^2} = \vert\Omega\vert\sqrt{R^2 - d^2} \sim 27.3\textrm{m/s} \end{displaymath}$

Come prima accennato, la reazione vincolare è opposta alla forza di Coriolis $2m\vec{\omega}\times\vec{v}$ . Ricordando che $\vec{v}=\dot{\rho}\ensuremath{\hat{e}_\rho}$ e che $\hat{\omega}\times\ensuremath{\hat{e}_\rho}= \ensuremath{\hat{e}_\varphi}$ otteniamo:

$\begin{displaymath} \vec{F_v} = -2m\dot{\rho}\omega\ensuremath{\hat{e}_\varphi} \end{displaymath}$

I moduli della reazioni vincolare nei due casi sono rispettivamente:

$\begin{displaymath} \left\{ \begin{array}{lll} \rho_f = 0 & \rightarrow & F_v ... ...ightarrow & F_v \sim 218.4\textrm{N} \\ \end{array} \right. \end{displaymath}$

In entrambi i casi la direzione è $-\ensuremath{\hat{e}_\varphi}$ moltiplicata per il segno di $\dot{\rho}$ (che è negativo nel primo caso e positivo nel secondo).

Vediamo ora una procedura di soluzione più complicata che non utilizza la conservazione dell'energia, ma determina la dinamica direttamente nel riferimento inerziale. Stavolta la coordinata azimutale $\varphi(t)$ è non banale e soddisfa la legge $\varphi=\omega t$ con $\omega$ costante poichè la biglia è vincolata a rimanere nella scanalatura. Il vettore posizione sarà quindi $\vec{r} = \rho \ensuremath{\hat{e}_\rho}$ . La velocità e la accelerazione si ottengono derivando questa espressione e ricordando le leggi di derivazione dei versori polari $\ensuremath{\hat{e}_\rho}= \dot{\varphi} \ensuremath{\hat{e}_\varphi}$ ed $\ensuremath{\hat{e}_\varphi}= - \dot{\varphi} \ensuremath{\hat{e}_\rho}$ e che la derivata di $\varphi$ rispetto al tempo è la costante $\omega$ per ipotesi

$\begin{displaymath} \left\{ \begin{array}{lll} \vec{v} & = & \dot{\rho} \ensur... ...dot{\rho}\ensuremath{\hat{e}_\varphi}\\ \end{array} \right. \end{displaymath}$

La forza agente sulla biglia sarà la somma della reazione vincolare della scanalatura $\vec{F}_v = F_v \ensuremath{\hat{e}_\varphi}$ , che ovviamente può agire solo ortogonalmente alla scanalatura, e della forza elastica della molla $-k\rho\ensuremath{\hat{e}_\rho}$ . La presenza della forza $\vec{F}_v$ implica che il sistema biglia più pallina non è isolato. Eguagliando componente per componente questa somma con $m\vec{a}$ otteniamo due equazioni scalari che ci permettono di determinare $\rho$ ed :

$\begin{displaymath} \left\{ \begin{array}{lll} F_v & = & 2m\omega\dot{\rho} \\... ... & = & m(\omega^2\rho - \ddot{\rho}) \\ \end{array} \right. \end{displaymath}$

La seconda delle due si può riscrivere come $\ddot{\rho} = - \Omega^2 \rho$ (ricordiamo che $\Omega^2$ è positiva o negativa a seconda che la velocità angolare $\omega$ sia minore o maggiore del valore limite trovato nel primo punto di questo esercizio). Nel caso che sia positiva (verificato da $\omega=50$ rad/s) l'equazione differenziale ha le ovvie soluzioni in seni e coseni, i coefficienti essendo determinati dalle condizioni iniziali $\rho(0)=d$ e $\dot{\rho}(0) = 0$ :

$\begin{displaymath} \rho(t) = d \cos(\Omega t) \end{displaymath}$

Questa soluzione descrive una biglia che nel riferimento rotante oscilla attorno al perno, con moto radiale armonico. La biglia interseca il perno per la prima volta al tempo $\tilde{t}$ tale che $\Omega \tilde{t} = \frac{\pi}{2}$ . Per ricavare il modulo della velocità nel riferimento inerziale ci basta sostituire questo valore del tempo nella espressione di $\vec{v}$ precedentemente trovata:

$\begin{displaymath} v_f = \vert\vec{v}(\,\tilde{t}\,)\vert = \vert\dot{\rho}(\,... ...mega = d \sqrt{\frac{k}{m} - \omega^2} \sim 17.7\textrm{m/s} \end{displaymath}$

Per coincidenza questo è lo stesso valore trovato precedentemente, perchè la differenza fra la velocità nel riferimento inerziale ed in quello non inerziale è $\omega\rho\ensuremath{\hat{e}_\varphi}$ , e nel caso $\rho_f=0$ questo termine si annulla. La reazione vincolare, il cui modulo invece non cambia al cambiare del sistema di riferimento, si ricava pure per sostituzione:

$\begin{displaymath} \vert\vec{F_v}(\,\tilde{t}\,)\vert = 2m\omega\vert\dot{\rho}(\,\tilde{t}\,)\vert = 2m\omega v_f \sim 70.8\textrm{N} \end{displaymath}$

La direzione della reazione vincolare è il limite di $-\ensuremath{\hat{e}_\varphi}$ (perchè $\dot{\rho}$ è negativa) per tempi prossimi a $\tilde{t}$ , che si vede subito essere $\hat{v}\times\hat{\omega}=\ensuremath{\hat{e}_\varphi}$ siccome la rotazione avviene in senso antiorario.

Nel caso che il disco ruoti con velocità angolare sufficientemente grande invece $\Omega$ è immaginario puro, e le soluzioni saranno espresse da esponenziali. Indicando con $\bar{\Omega}$ la parte immaginaria di $\Omega$ otteniamo:

$\begin{displaymath} \rho(t) = Ae^{\bar{\Omega}t} + Be^{-\bar{\Omega}t} \end{displaymath}$

I coefficienti di nuovo si ricavano imponendo le condizioni iniziali, per cui otteniamo le seguenti espressioni per la posizione e la velocità radiale:

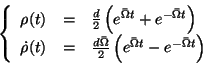
$\begin{displaymath} \left\{ \begin{array}{lll} \rho(t) & = & \frac{d}{2} \lef... ...mega}t} - e^{-\bar{\Omega}t} \right) \\ \end{array} \right. \end{displaymath}$

La distanza dal perno ora cresce col tempo, e raggiunge il bordo del disco al tempo tale che $\rho(t')=R$ :

$\begin{displaymath} R = \rho(t') = \frac{d}{2}\left( e^{\bar{\Omega}t} + e^{-\bar{\Omega}t} \right) \end{displaymath}$

Questa è una equazione trascendentale, non risolubile in modo banale. Possiamo comunque ricavare $\dot{\rho}$ sommando e sottraendo le equazioni per $\rho$ e $\dot{\rho}$ dopo avere moltiplicato la prima per $\bar{\Omega}$ :

$\begin{displaymath} \left\{ \begin{array}{lll} \bar{\Omega}\rho(t) + \dot{\rho... ...& d \bar{\Omega}e^{-\bar{\Omega}t} \\ \end{array} \right. \end{displaymath}$

Ponendo ora , $\rho(t')=R$ , $\dot{\rho}(t')=\dot{\rho}_f$ ed eguagliando le due espressioni per $e^{\bar{\Omega}t'}$ otteniamo:

$\begin{displaymath} \bar{\Omega}^2R^2 - \dot{\rho}_f^2 = d^2 \bar{\Omega}^2 \q... ...arrow \quad\quad \dot{\rho}_f = \bar{\Omega}\sqrt{R^2 - d^2} \end{displaymath}$

che è l'espressione già trovata per la velocità nel riferimento non inerziale. Nel riferimento inerziale è necessario aggiungere la componente azimutale:

$\begin{displaymath} \vec{v}(t') = \bar{\Omega}\sqrt{R^2 - d^2}\ensuremath{\hat{... ...2\omega^2 + R^2\Omega^2 - d^2\Omega^2} \sim 65.9\textrm{m/s} \end{displaymath}$

La reazione vincolare si ricava come prima.

Esercizio 7
Se la scalatrice perde la presa un attimo prima di moschettonare un chiodo, si trova ad avere un lasco pari alla distanza fra i due chiodi. Essa cadrà quindi in verticale per una distanza pari a prima di cominciare a tendere la corda; durante la fase di allungamento poi scenderà ancora per una distanza pari all'allungamento totale della corda $\Delta$ . L'energia potenziale gravitazionale corrispondente deve essere dissipata elasticamente dalla corda. Il massimo allungamento $\Delta$ della corda determina quindi la massima distanza fra i chiodi:

$\begin{displaymath} 2mgd = \frac{1}{2}k\Delta^2 - mg\Delta \quad\quad \rightar... ... d = \frac{\Delta}{2} \left( \frac{k\Delta}{2mg} - 1 \right) \end{displaymath}$

Consideriamo un modello di scalata dove la corda è fissata ai moschettoni; in questo modello la trazione esercitata sul chiodo é pari alla tensione della corda. Nel momento di massimo allungamento la trazione sul chiodo è quindi massima e $\Delta_\textrm{\tiny max}= T_\textrm{\tiny max}/k$ . Sostituendolo nella relazione precedente otteniamo che la distanza massima fra due chiodi (nella sola ipotesi di non voler rompere il chiodo, lasciamo perdere la schiena ...) è:

$\begin{displaymath} d_\textrm{\tiny max}= \frac{T_\textrm{\tiny max}}{2k} \lef... ...c{T_\textrm{\tiny max}}{2gm} - 1 \right) \sim 11.8\textrm{m} \end{displaymath}$

Nella fase libera della caduta, la scalatrice acquista una velocità pari a $v_0=\sqrt{4gd}$ [Dopo la modifica del testo questa è la velocità a cui siamo interessi, e vale $v_0 \sim 14.00$ m/s. Nel seguito verranno comunque riportate le soluzioni ad entrambe le domande]. Quando la corda entra in tensione poi l'accelerazione di gravità viene contrastata dalla forza elastica. L'equazione di conservazione dell'energia, chiamando $\delta$ l'allungamento della corda, ci dice:

$\begin{displaymath} \frac{1}{2}mv_0^2 = \frac{1}{2}mv^2 - mg\delta + \frac{1}{... ...w \quad\quad v = \sqrt{4gd + 2g\delta - \frac{k\delta^2}{m}} \end{displaymath}$

avendo posto lo zero dell'energia potenziale gravitazionale nel punto in cui la corda si comincia a tendere. Per ricavare il valore massimo della velocità deriviamo rispetto a $\delta$ ed imponiamo il risultato uguale a zero:

$\begin{displaymath} 0 = \frac{dv}{d\delta} = \frac{1}{2v}(2g - 2\frac{k\delta}{m}) \quad\quad \rightarrow \quad\quad \delta = \frac{mg}{k} \end{displaymath}$

$\begin{displaymath} \rightarrow \quad\quad v_\textrm{\tiny max}= v(\delta_\tex... ... max}) = \sqrt{4gd + \frac{mg^2}{k}} \sim 14.06\textrm{m/s} \end{displaymath}$

Per ricavare l'allungamento della corda quando la velocità della scalatrice si dimezza rispetto al valore massimo [nella versione modificata, al valore ] sostituiamo $v=v_{1/2}=v_\textrm{\tiny max}/2$ [nella versione modificata, $v=v_{1/2}=v_0/2$ ] dentro l'equazione di conservazione dell'energia e risolviamo rispetto a $\delta$ :

$\begin{displaymath} \frac{1}{2}mv_0^2 = \frac{1}{2}m(\frac{v_\textrm{\tiny max... ...rac{2mg}{k}\delta + \frac{m^2g^2}{4k^2} - \frac{3mgd}{k} = 0 \end{displaymath}$

$\begin{displaymath} \rightarrow \quad\quad \delta_{1/2} = \frac{mg}{k} \pm \sqrt{ \frac{3m^2g^2}{4k^2} + \frac{3mgd}{k} } \sim 1.68\textrm{m} \end{displaymath}$

[Quando $v_{1/2}=v_0/2$ lo stesso procedimento restituisce:

$\begin{displaymath} \rightarrow \quad\quad \delta_{1/2} = \frac{mg}{k} \pm \sqrt{ \frac{m^2g^2}{k^2} + \frac{3mgd}{k} } \sim 1.68\textrm{m} \end{displaymath}$

ed il valore numerico è praticamente lo stesso.] La soluzione prescelta è quella con il segno positivo (l'altra corrisponde al rimbalzo sopra il punto di lasco e comunque non è significativa perchè la conservazione dell'energia come scritta prima vale per $\delta>0$ , siccome la corda può solo spingere, non tirare). La trazione quando $v=v_{1/2}$ vale:

$\begin{displaymath} T_{1/2} = k\delta_{1/2} \sim 5882\textrm{N} \end{displaymath}$

Quando la scalatrice arriva a fermarsi ritroviamo l'equazione precedente per $\Delta$ che ha soluzione:

$\begin{displaymath} \Delta = \frac{mg}{k} \pm \sqrt{\frac{m^2g^2}{k^2}+\frac{4mgd}{k}} \sim 1.92\textrm{m} \end{displaymath}$

Il segno positivo nell'equazione di secondo grado è stato scelto per gli stessi motivi precedenti. La trazione nel punto di velocità nulla è infine:

$\begin{displaymath} T_0 = k\Delta \sim 6707\textrm{N} \end{displaymath}$

Ritorniamo ora sul modello precedente; cioè che non è realistico è che la corda sia fissa ai moschettoni: piuttosto la corda scorre dentro i moschettoni usandoli come ``carrucole''. In questo caso la trazione esercitata sul chiodo é pari al doppio della tensione della corda. Questo si può capire perchè possiamo immaginare la corda come costituita da due sistemi (le due metà della corda) che si uniscono all'altezza del moschettone: ognuno dei due sistemi esercita sul moschettone una trazione pari alla tensione della corda (identica in una corda ideale nei due spezzoni). Nel caso in cui la corda fosse legata al moschettone, lo spezzone che va dal moschettone a terra non è in tensione quando la scalatrice cade, e questo determina il fattore di differenza. Quello che cambia nei calcoli precedenti è solo la formula per la massima distanza fra i chiodi per prevenirne la rottura in caso di caduta, dove si deve porre $\Delta_\textrm{\tiny max}= T_\textrm{\tiny max}/2k$ , ovvero:

$\begin{displaymath} d_\textrm{\tiny max}= \frac{T_\textrm{\tiny max}}{4k} \lef... ...c{T_\textrm{\tiny max}}{4gm} - 1 \right) \sim 2.60\textrm{m} \end{displaymath}$

Esercizio 8

In questo esercizio stiamo considerando un moto circolare uniforme dove l'accelerazione centripeta è data dall'accelerazione che il campo gravitazionale terrestre impone ad una distanza pari a $R_{TL}$ . Ricaviamo immediatamente la velocità lineare ed angolare:

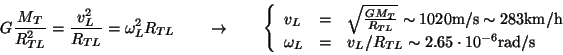
$\begin{displaymath} G \frac{M_T}{R^2_{TL}} = \frac{v_L^2}{R_{TL}} = \omega^2_L ... ... \sim 2.65\cdot10^{-6}\textrm{rad/s} \\ \end{array} \right. \end{displaymath}$

Il periodo di rivoluzione della Luna attorno alla Terra viene immediatamente dal tempo necessario a coprire un angolo giro con la precedente velocità angolare:

$\begin{displaymath} T_L = \frac{2\pi}{\omega_L} \sim 2.37\cdot10^{6}\textrm{s} \sim 27.4\textrm{~giorni} \end{displaymath}$

Sapendo che l'accelerazione di gravità sulla superficie di un pianeta di massa e raggio vale , ed usando l'accelerazione di gravità sulla superficie della terra come accelerazione campione, possiamo scrivere:

$\begin{displaymath} g_L = g_T \frac{M_L}{M_T}\left(\frac{R_T}{R_L}\right)^2 \sim .165 g_T \sim 1.62 \textrm{m/s$^2$} \end{displaymath}$

La velocità di fuga da un pianeta è quella velocità tale che l'energia cinetica è in grado di compensare la variazione di energia potenziale dalla superficie del pianeta all'infinito. Siccome lo zero dell'energia potenziale gravitazionale è solitamente posto all'infinito, questo equivale a dire:

$\begin{displaymath} \frac{1}{2}mv^2_f = G\frac{Mm}{R} \quad\quad \rightarrow \quad\quad v_f = \sqrt{\frac{2MG}{R}} \end{displaymath}$

Nel caso della velocità di fuga dalla Luna abbiamo:

$\begin{displaymath} v_{f_L} = \sqrt{\frac{2M_LG}{R_L}} \sim 2.37\textrm{km/s} \end{displaymath}$

Per rispondere all'ultima domanda, consideriamo un riferimento solidale con la Terra (nella nostra approssimazione questo è inerziale). In questo riferimento un corpo sulla superficie della Luna ha un'energia potenziale gravitazionale combinata fra Terra e Luna pari a:

$\begin{displaymath} V = -G\frac{mM_T}{R_{TL}} - G\frac{mM_L}{R_L} \end{displaymath}$

La velocità necessaria per allontanarsi indefinitamente è dunque tale che:

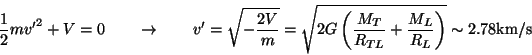
$\begin{displaymath} \frac{1}{2}m{v'}^2 + V = 0 \quad\quad \rightarrow \quad\qu... ..._T}{R_{TL}} + \frac{M_L}{R_L}\right)} \sim 2.78\textrm{km/s} \end{displaymath}$

La massima velocità relativa alla Terra di un corpo che si muova con velocità $v_{f_L}$ rispetto alla Luna è $v' = v_{f_L} + v_L \sim 3.39\textrm{km/s}$ , quindi un corpo con velocità $v_{f_L}$ rispetto alla Luna può effettivamente, se opportunamente direzionato, allontanarsi indefinitamente anche dalla Terra.

Esercizio n. 9

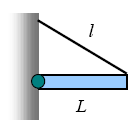
Le tre forze necessariamente costituiscono un sistema di forze concorrenti (e complanari). E’ pertanto sufficiente richiedere che si annulli il risultante vettoriale delle tre forze per ottenere l’equilibrio statico del sistema. Nel caso in esame, detto a l’angolo fra la fune e la parete verticale, detta T la tensione della fune ed R la reazione al perno liscio si proietta secondo gli assi parallelo e perpendicolare alla mensola per trovare che

P = ( T + R ) cos a (lungo la direzione perpendicolare)

R sin a = T sin a (lungo la direzione parallela).

Risolvendo in funzione di a si ottiene

R = T = P / ( 2 cos a).

Essendo

sin a = L / l

si può anche scrivere

R = T = P l / [2 ( l²- L² )1/2].

(Prof. Stefano Oss)

Stefano Bettelli 2001-01-24

Testi problemi vari