Next: Soluzioni proposte
Previous: Esercitazioni di Geometria I 1998/99
Geometria 1
Primo appello, sessione invernale, a.a. 1998/99
9 febbraio 2000
Si ricorda che, anche se non esplicitamente richiesto nei testi, tutte le
risposte alle domande devono essere adeguatamente motivate con
dimostrazioni o confutazioni.
Esercizio 1
Siano dati in
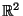
le rette:
Dire se esiste
- 1.
- un'affinità
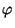 di
di
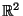 tale che
tale che
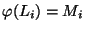 per ogni i;
per ogni i;
- 2.
- un'affinità
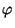 di
di
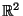 tale che
tale che
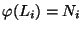 per ogni i.
per ogni i.
In caso di risposta affermativa la si determini e se ne discuta l'unicità.
Soluzione
Esercizio 2
Siano
r e
s le rette in
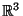
definite da:
e
P=(1,2,1). Dire se esiste:
- 1.
- una retta passate per P e parallela a r e s;
- 2.
- una retta passante per P ed incidente a r e s.
In caso di risposta affermativa la si determini e se ne discuta l'unicità.
Soluzione
Esercizio 3
Siano dati i quattro punti
Si determini il fascio delle coniche per
P1,
P2,
P3 e
P4.
Tra le coniche di tale fascio si determini quella passante per il punto
P5=(1,1) e se ne studi il tipo affine.
Soluzione
Esercizio 4
Nello spazio vettoriale reale
V dei polinomi di grado minore o uguale a 2 si
consideri il prodotto scalare definito da:
Se ne determinino la segnatura ed una base ortogonale.
Soluzione
Esercizio 5
Sia
V uno spazio vettoriale reale di dimensione finita,
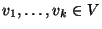
e
sia
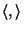
il prodotto scalare su
V* (il duale di
V) definito da
Si provi che
- 1.
-
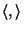 è semidefinito positivo:
è semidefinito positivo:
- 2.
-
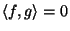 per ogni
per ogni 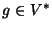 se e solo se
se e solo se
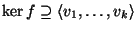 :
:
- 3.
-
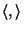 è definito positivo se e solo se
è definito positivo se e solo se
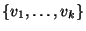 è
un sistema di generatori di V.
è
un sistema di generatori di V.
Soluzione



Next: Soluzioni proposte
Previous: Esercitazioni di Geometria I 1998/99
Domenico Luminai
2000-02-14
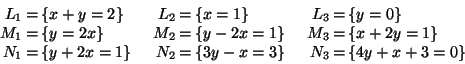
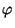 di
di
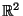 tale che
tale che
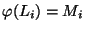 per ogni i;
per ogni i;
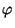 di
di
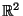 tale che
tale che
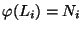 per ogni i.
per ogni i.