



Next: Geometria 8 febbraio. Tema
Up: Esercizi
Previous: Geometria affine e metrica
Indice
Esercizio 69
Determinare gli autovalori di una matrice quadrata triangolare superiore.
Dimostrazione.
Sia
una matrice
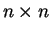
triangolare superiore.
Il polinomio caratteristico di  è il determinante di
è il determinante di
Poichè
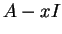
è ancora una matrice triangolare superiore il suo determinante
è il prodotto degli
elementi sulla diagonale principale, ovvero:
Gli autovalori di

sono le radici di
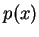
ovvero gli elementi sulla
sua diagonale principale:
Allo stesso risultato si perviene se la matrice è diagonale inferiore ovvero della forma

Esercizio 70
Sia

l'endomorfismo di
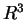
tale che
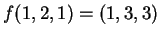
,
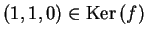
e
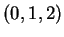
è un
autovettore relativo all'autovalore

. Discutere la diagonalizzabilità di

.
Dimostrazione.
I vettori
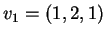
,

e
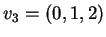
formano una base di
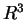
. Inoltre si ha
Scegliendo la base
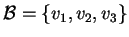
nel dominio e nel codominio la
matrice associata ad

è :
La matrice

è triangolare inferiore sicchè i suoi autovalori sono gli
elementi sulla diagonale principale. Segue che

ammette l'autovalore

con
molteplicità algebrica
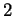
e l'autovalore 0 con molteplicità algebrica

.
Il vettore 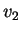 è un autovettore relativo all'autovalore 0 sicchè
il relativo autospazio,
è un autovettore relativo all'autovalore 0 sicchè
il relativo autospazio, 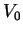 , è generato da
, è generato da 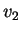 :
:
Il vettore 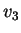 è un autovettore relativo all'autovalore
è un autovettore relativo all'autovalore  . D'altra parte
l'autospazio,
. D'altra parte
l'autospazio, 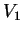 , relativo all'autovettore
, relativo all'autovettore  è il nucleo di
è il nucleo di 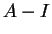 .
.
Ora
e la matrice
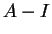
ha rango due sicchè il suo nucleo ha dimensione

.
Segue che
e pertanto

non è diagonalizzabile.

Esercizio 71
Sia

la matrice:
- Determinare autovalori e autospazi di
 .
.
- Determinare, se possibile, una base di autovettori.
Verificare che la matrice è radice del suo polinomio caratteristico.
Dimostrazione.
La matrice

è triangolare inferiore sicchè i suoi autovalori sono gli
elementi sulla diagonale principale.
La matrice  ammette allora l'autovalore
ammette allora l'autovalore  con molteplicità algebrica
con molteplicità algebrica 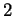 e
l'autovalore
e
l'autovalore 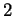 con molteplicità algebrica
con molteplicità algebrica  .
.
L'autospazio relativo all'autovalore  è il nucleo della matrice :
è il nucleo della matrice :
ovvero
Poichè la dimensione di
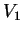
è
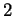
(e la dimensione di
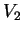
è
necessariamente

) possiamo dedurre che

è diagonalizzabile.
Infine l'autospazio relativo all'autovalore 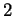 è il nucleo della matrice
è il nucleo della matrice
e pertanto
Infine una base di autovettori si ottiene come unione delle basi dei due autospazi:

Esercizio 72
Date le matrici:
- Determinare autovalori e autospazi di
 e
e 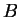 rispettivamente.
rispettivamente.
- Determinare, se possibile, una base di autovettori.
Dimostrazione.
Il polinomio caratteristico della matrice

è:
sicchè la matrice

ammette l'autovalore
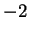
con molteplicità algebrica
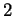
e
l'autovalore
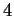
con molteplicità algebrica

.
L'autospazio relativo all'autovalore 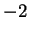 è il nucleo di
è il nucleo di
ovvero
Poichè
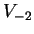
ha dimensione
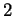
la matrice è diagonalizzabile.
L'autospazio relativo all'autovalore 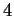 è il nucleo di
è il nucleo di
pertanto
Infine una base di
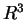
formata da autovettori di

è, per esempio, l'insieme:
Il polinomio caratteristico della matrice 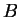 è:
è:
sicchè anche la matrice
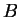
ammette l'autovalore
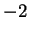
con molteplicità algebrica
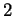
e
l'autovalore
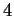
con molteplicità algebrica

.
L'autospazio relativo all'autovalore 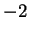 è il nucleo della matrice
è il nucleo della matrice
che, ridotta a gradino, diventa:
Ne segue che
La matrice
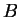
non è quindi diagonalizzabile perchè la dimensione di
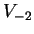
è

.
Infine determiniamo l'autospazio relativo all'autovalore 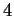 . Si tratta di determinare il nucleo
della matrice:
. Si tratta di determinare il nucleo
della matrice:
che, ridotta a gradino, diventa:
L'autospazio relativo a
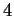
è allora il sottospazio:
Infine poichè
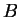
non è diagonalizzabile non si può determinare una base di
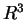
formata da autovettori di
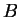
.

Esercizio 73
Sia
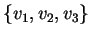
una base di
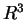
e sia
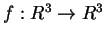
l'endomorfismo definito da:
Determinare autovalori e autospazi di

. Determinare, se possibile, una base
di autovettori. Verificare che autovettori relativi ad autovalori distinti sono
tra loro ortogonali.
Dimostrazione.
La matrice di

ripsetto alla base
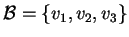
è la matrice
e il suo polinomio caratteristico è
Poichè si tratta di una matrice
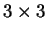
con tre autovalori distinti è sicuramente
diagonalizzabile.
Determiniamo ora gli autospazi di  . Si ha:
. Si ha:
e
Una base di
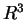
costituita da autovettori di

è :
Infine verifichiamo che autovettori relativi ad autovalori distinti sono ortogonali, ovvero che
il loro prodotto scalare è nullo.
Abbiamo
per ogni
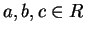
.

Esercizio 74
Mostrare che un endomorfismo
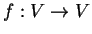
ha come autovalore 0 se e solo se

non è iniettivo.
Dimostrazione.
Se

ha come autovalore 0 allora, per definizione, esiste un vettore
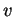
non nullo tale che
pertanto
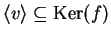
.
D'altra parte questo implica che  non è iniettivo perchè per ogni
non è iniettivo perchè per ogni 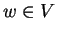
e
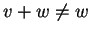
.
Viceversa se  non è iniettivo allora esistono
non è iniettivo allora esistono 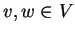 con
con
e
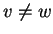
. Posto
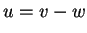
, il vettore
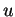
è non nullo e
sicchè

ammette l'autovalore 0.

Esercizio 75
Siano

e
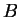
due matrici quadrate
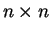
. Provare che
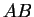
e
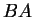
hanno
gli stessi autovalori.
Dimostrazione.
Supponiamo che
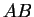
ammetta l'autovalore 0. Questo significa che esiste un
vettore non nullo
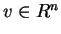
tale che
In altre parole esiste una soluzione non banale del sistema omogeneo
D'altra parte il sistema appena scritto ha soluzioni non banali se e solo se
Ora
sicchè anche il determinante di
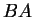
è nullo. Questo significa che anche il
sistema
ammette soluzioni non banali ovvero che 0 è un autovalore di
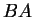
.
Supponiamo adesso che la matrice 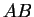 ammetta un autovalore
ammetta un autovalore
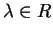 non
nullo. Allora esiste
non
nullo. Allora esiste 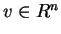 non nullo tale che
non nullo tale che
Sia
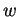
il vettore
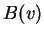
. Risulta:
Per poter concludere che
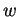
è un autovettore di
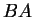
relativo all'autovalore
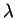
rimane
solo da provare che
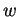
non è il vettore nullo.
D'altra parte se fosse 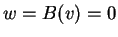 avremmo
avremmo
mentre abbiamo per ipotesi che
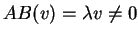
.
Abbiamo quindi provato che ogni autovalore di 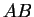 è autovalore anche di
è autovalore anche di 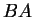 . Con
ragionamento analogo si prova che ogni autovalore di
. Con
ragionamento analogo si prova che ogni autovalore di 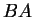 è autovalore di
è autovalore di 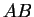 .
.

Esercizio 76
Sia
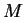
la matrice:
con
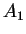
e
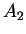
matrici quadrate. Mostrare che il polinomio caratteristico di
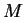
è il prodotto dei polinomi caratteristici di
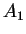
e
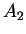
.
Dimostrazione.
Osserviamo innanzitutto che la matrice
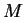
deve essere una matrice quadrata
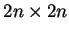
.
Il polinomio caratteristico di 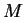 è:
è:
D'altra parte la matrice identità
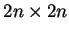
si può guardare come una matrice a blocchi:
dove
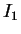
e
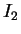
sono matrici identità
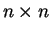
.
Allora

Esercizio 77
Determinare per quali valori del parametro reale
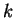
la matrice
è diagonalizzabile. Determinare, se possibile, una base di autovettori.
Dimostrazione.
La matrice è triangolare superiore quindi gli autovalori sono tutti e soli gli elementi sulla
diagonale principale:
Per
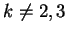
gli autovalori sono tutti distinti sicchè la matrice è diagonalizzabile.
Inoltre
e
Notiamo che nel determinare gli autospazi abbiamo usato l'ipotesi che
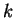
fosse diverso da
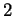
e
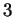
.
Una base di autovettori è
Esaminiamo ora i casi
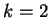
e
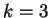
.
Per 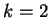 la matrice
la matrice  diventa:
diventa:
Per verificare che sia diagonalizzabile basta verificare se la dimensione dell'autospazio
relativo a
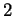
è uguale a
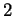
.
Ora:
Segue che
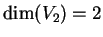
e

è diagonalizzabile.
Una base di autovettori è :
Infine per 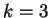 la matrice
la matrice  diventa:
diventa:
Di nuovo guardiamo all'autospazio relativo a
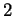
:
dunque

è diagonalizzabile e una base di autovettori è:
Notiamo che gli autovalori per
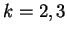
sono
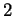
e
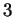
.

Esercizio 78
Sia
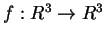
l'endomorfismo definito da:
Determinare autovalori e autovettori di

. Determinare, se possibile, una base
di autovettori.
Dimostrazione.
La matrice di

rispetto alla base canonica è;
Il polinomio caratteristico di

è
Gli autovalori di

sono
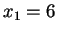
con molteplicità algebrica

e
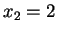
con
molteplicità
algebrica
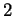
.
L'autospazio relativo all'autovalore 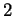 è:
è:
Poichè
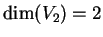
la matrice è diagonalizzabile.
L'autospazio relativo all'autovalore 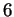 è:
è:
Infine una base di
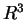
costituita da autovettori di

è l'insieme:

Esercizio 79
Date le matrici
determinare, se possibile, due matrici
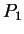
e
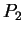
tali che
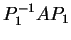
e
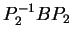
siano matrici diagonali.
Dimostrazione.
Una matrice
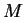
quadrata di ordine
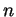
, è diagonalizzabile se e solo se esiste una matrice
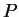
invertibile tale che
sia una matrice diagonale.
Se
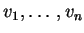 sono
sono 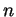 autovettori di
autovettori di 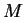 linearmente indipendenti, la matrice
linearmente indipendenti, la matrice 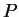 le cui
colonne sono i vettori
le cui
colonne sono i vettori 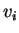 ,
,
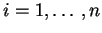 , è invertibile e
, è invertibile e 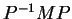 è una matrice
diagonale.
è una matrice
diagonale.
Consideriamo ora la matrice  . Il suo polinomio caratteristico è:
. Il suo polinomio caratteristico è:
sicchè i suoi autovalori sono
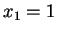
con molteplicità algebrica

e
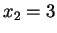
con molteplicità algebrica
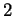
.
L'autospazio relativo all'autovalore 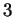 è il sottospazio:
è il sottospazio:
L'autospazio relativo all'autovalore

è, invece, il sottospazio:
Una base di
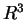
formata da autovettori di

è l'insieme:
e la matrice
è tale che
La matrice
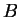
ammette l'unico autovalore

con molteplicità algebrica
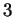
.
D'altra parte non è diagonalizzabile infatti l'autospazio relativo ad  è:
è:
Poichè
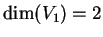
non si può determinare una base di
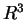
costituita da autovettori di
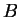
e dunque non si può determinare una matrice
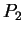
tale che
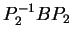
sia una matrice diagonale.

Esercizio 80
Sia
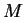
una matrice quadrata e simmetrica con un solo autovalore
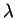
.
Provare che
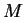
coincide con la matrice
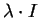
, dove
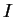
è la
matrice identità.
Dimostrazione.
La matrice
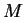
è simmetrica e dunque diagonalizzabile. Inoltre
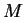
ha il solo
autovalore
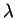
, e quindi è simile alla matrice
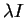
.
Esiste allora un
matrice invertibile 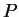 tale che:
tale che:
Moltiplicando l'uguaglianza appena scritta a sinistra per
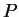
otteniamo:
Moltiplicando quest'ultima a destra per
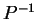
otteniamo:
ovvero che
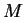
è una matrice diagonale.

Compiti di Esame




Next: Geometria 8 febbraio. Tema
Up: Esercizi
Previous: Geometria affine e metrica
Indice
Andreatta Marco
2000-09-18

![]() è il determinante di
è il determinante di
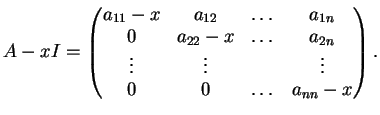
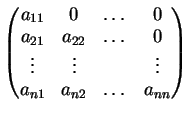

![]() è il determinante di
è il determinante di
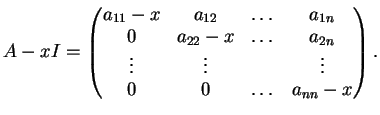
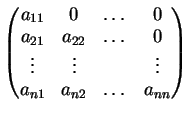
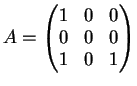
![]() è un autovettore relativo all'autovalore 0 sicchè
il relativo autospazio,
è un autovettore relativo all'autovalore 0 sicchè
il relativo autospazio, ![]() , è generato da
, è generato da ![]() :
:
![]() è un autovettore relativo all'autovalore
è un autovettore relativo all'autovalore ![]() . D'altra parte
l'autospazio,
. D'altra parte
l'autospazio, ![]() , relativo all'autovettore
, relativo all'autovettore ![]() è il nucleo di
è il nucleo di ![]() .
.
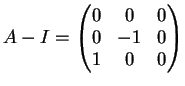
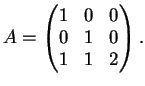
![]() ammette allora l'autovalore
ammette allora l'autovalore ![]() con molteplicità algebrica
con molteplicità algebrica ![]() e
l'autovalore
e
l'autovalore ![]() con molteplicità algebrica
con molteplicità algebrica ![]() .
.
![]() è il nucleo della matrice :
è il nucleo della matrice :
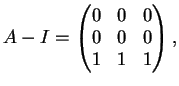
![]() è il nucleo della matrice
è il nucleo della matrice
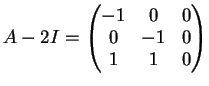
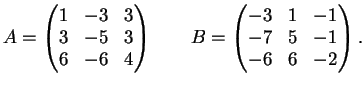
![]() è il nucleo di
è il nucleo di
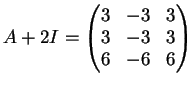
![]() è il nucleo di
è il nucleo di
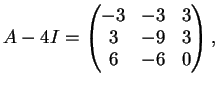
![]() è:
è:
![]() è il nucleo della matrice
è il nucleo della matrice
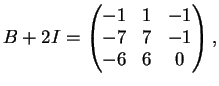
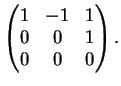
![]() . Si tratta di determinare il nucleo
della matrice:
. Si tratta di determinare il nucleo
della matrice:
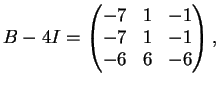
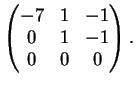
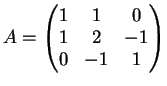
![]() . Si ha:
. Si ha:
![]() non è iniettivo perchè per ogni
non è iniettivo perchè per ogni ![]()
![]() non è iniettivo allora esistono
non è iniettivo allora esistono ![]() con
con
![]() ammetta un autovalore
ammetta un autovalore
![]() non
nullo. Allora esiste
non
nullo. Allora esiste ![]() non nullo tale che
non nullo tale che
![]() avremmo
avremmo
![]() è autovalore anche di
è autovalore anche di ![]() . Con
ragionamento analogo si prova che ogni autovalore di
. Con
ragionamento analogo si prova che ogni autovalore di ![]() è autovalore di
è autovalore di ![]() .
.
![]()
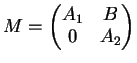
![]() è:
è:
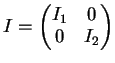
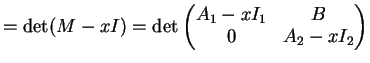
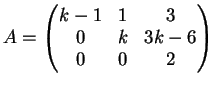
![]() la matrice
la matrice ![]() diventa:
diventa:
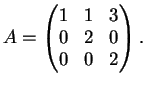
![]() la matrice
la matrice ![]() diventa:
diventa:
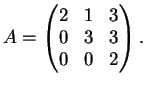
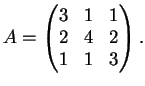
![]() è:
è:
![]() è:
è:
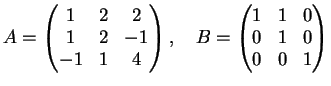
![]() sono
sono ![]() autovettori di
autovettori di ![]() linearmente indipendenti, la matrice
linearmente indipendenti, la matrice ![]() le cui
colonne sono i vettori
le cui
colonne sono i vettori ![]() ,
,
![]() , è invertibile e
, è invertibile e ![]() è una matrice
diagonale.
è una matrice
diagonale.
![]() . Il suo polinomio caratteristico è:
. Il suo polinomio caratteristico è:
![]() è il sottospazio:
è il sottospazio:
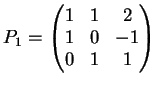
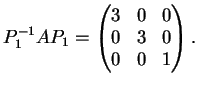
![]() è:
è:
![]() tale che:
tale che:
![]()