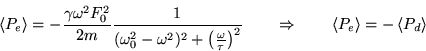Analisi della potenza immessa a regime

In un oscillatore armonico forzato e smorzato, a regime, per definizione, la potenza media dissipata dalla forza di attrito viscoso deve essere compensata dalla potenza media immessa nell'oscillatore dalla forza di eccitazione. Intendiamo ora verificare questa affermazione esplicitamente. Calcoliamo per prima la potenza media, $P_d$, dissipata dalla forza di attrito viscoso $F_a$:

$$F_a = - m \gamma v \ensuremath{\quad\quad \Rightarrow \quad\quad}P_d = - m \gamma v^2$$

Quindi, per ricavare questa potenza dobbiamo avere una espressione esplicita per la velocità. Partendo dalla legge del moto del nostro oscillatore, $x(t) = A \cos(\omega t + \varphi)$, e derivando otteniamo:

$$v = \frac{dx}{dt} = - A \omega \sin(\omega t + \varphi)$$

La potenza media dissipata risulta dunque: $$\ensuremath{\langle P_d \rangle}%%= \media{- m \gamma v^2} ... ...ga t + \varphi) \rangle} = -\frac{1}{2} m \gamma A^2 \omega^2$$ dove nell'ultimo passaggio è stato sostituito il valore medio nel tempo del quadrato di una sinuoside con argomento lineare nel tempo, che è $1/2$, indipendentemente dalla sua fase: $$\ensuremath{\langle \sin^2(\omega t + \varphi) \rangle}= \frac{1}{2}$$

Ricordando che (vedere equazione 3):

$$A = \frac{F_0/m}{\sqrt{(\omega_0^2-\omega^2)^2 + \left(\frac{\omega}{\tau}\right)^2}}$$

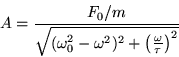
si ricava che:

$$\ensuremath{\langle P_d \rangle}= - \frac{\gamma \omega^2 F... ...{(\omega_0^2-\omega^2)^2 + \left(\frac{\omega}{\tau}\right)^2}$$

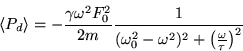
Consideriamo ora la potenza immessa dalla forza di eccitazione:

$$F = F_0 \cos(\omega t) \ensuremath{\quad\quad \Rightarrow \... ...= Fv = - A \omega F_0 \cos(\omega t) \sin(\omega t + \varphi)$$

La potenza immessa dipende quindi fortemente dalla differenza di fase fra la velocità e la forza di eccitazione. Sviluppiamo ora il prodotto di queste due quantità:

$$\begin{eqnarray*} \cos(\omega t) \sin(\omega t + \varphi) & = & {\cos(\omega t... ...\cos(\varphi) \sin(2\omega t) + \sin(\varphi) \cos^2(\omega t)} \end{eqnarray*}$$

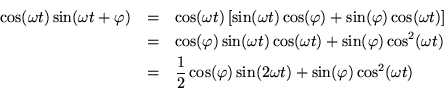
Per ottenere il valore medio nel tempo di questa quantità è sufficiente notare, come prima, che se l'argomento è lineare nel tempo, il quadrato di una funzione sinusoidale media ad un mezzo, indipendentemente dalla fase, e una sinusoide media a zero. Quindi:

$$\ensuremath{\langle \cos(\omega t) \sin(\omega t + \varphi)... ...th{\langle P_e \rangle}= - \frac{AF_0 \omega}{2} \sin(\varphi)$$

Determiniamo ora $A \sin(\varphi)$. È immediato notare che questa quantità è la parte immaginaria dell'ampiezza complessa $x_0 = A e^{i\varphi}$. Ricordando l'equazione (2) otteniamo allora:

$$A \sin(\varphi) = \ensuremath{\mathbf{Im}}\left( {x_0} \rig... ...{(\omega_0^2-\omega^2)^2 + \left(\frac{\omega}{\tau}\right)^2}$$

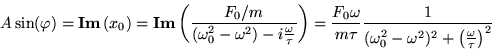
Ricordando anche che $\tau = \frac{1}{\gamma}$, l'espressione della potenza di eccitazione diviene:

$$\ensuremath{\langle P_e \rangle} = - \frac{\gamma \omega^2 ... ...math{\langle P_e \rangle}= - \,\ensuremath{\langle P_d \rangle}$$

come volevasi dimostrare.