La funzione di Plank

La funzione di Plank è definita come:

$$Y = - \frac{G}{T} = S - \frac{H}{T}$$

Possiamo considerare il differenziale di $Y$ rispetto a $T$ e $P$ utilizzando l'espressione $dH=T dS+V dP$ (vedere l'equazione 9) per l'entalpia:

$$dY = dS - \frac{dH}{T} + \frac{H}{T^2}\,dT \ensuremath{\qu... ...ightarrow \quad\quad} dY = \frac{H}{T^2}\,dT - \frac{V}{T}\,dP$$

Questa espressione ci permetterà di trovare una relazione fra processi reversibili isotermi (dove $T$ non varia) ed isobari (dove $P$ non varia). Anche per la funzione di Plank possiamo differenziare rispetto a $T$ e $P$ ed ottenere per confronto diretto le derivate parziali:

$$dY = \ensuremath{\left( \ensuremath{\frac{\partial{Y}}{\par... ...\frac{\partial{Y}}{\partial{P}}} \right)_{\!T}}= - \frac{V}{T}$$

Applicando allora la relazione di Schwarzt otteniamo:

$$\left[ \ensuremath{\ensuremath{\frac{\partial{}}{\partial{P... ...suremath{\frac{\partial{}}{\partial{T}}}}\frac{V}{T} \right)_P$$

L'utilità della funzione di Plank si basa sul fatto che essa può essere usata per trovare la variazione della funzione di Gibbs $G$. Infatti:

$$\frac{H}{T^2} = \ensuremath{\left( \ensuremath{\frac{\parti... ...emath{\frac{\partial{\frac{G}{T}}}{\partial{T}}} \right)_{\!P}}$$

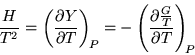
che in forma integrale diventa:

$$G = - T \left( Y_0 + {\int_{\makebox[0pt]{\textrm{\tiny\rule{0pt}{3\baselineskip}{isobara~~}}}}} \frac{H}{T^2}\,dT \right)$$

dove l'integrazione viene eseguita a $P$ costante e $Y_0$ è una costante di integrazione.