La funzione entropia

Ricordiamo che la funzione entropia è il differenziale esatto definito da:

$$dS = \frac{\omega}{T}$$

dove $\omega = dU + P dV$ è la forma differenziale ``calore'', per una trasformazione reversibile. Sviluppiamo ora $dU$ considerando $U$ come funzione di $V$ e $T$ e raccogliamo rispetto a $dV$ e $dT$:

$$dS = \frac{dU + P dV}{T} = \frac{1}{T} \ensuremath{\left(... ...th{\frac{\partial{U}}{\partial{V}}} \right)_{\!T}}\right] dV$$

Considerando anche $S$ una funzione di $V$ e $T$, otteniamo per confronto diretto che:

$$\ensuremath{\left( \ensuremath{\frac{\partial{S}}{\partial{... ...ft( \ensuremath{\frac{\partial{U}}{\partial{V}}} \right)_{\!T}}$$

Applicando allora la relazione di Schwartz ricaviamo l'identità:

$$\left\{ \ensuremath{\ensuremath{\frac{\partial{}}{\partial{... ...ac{\partial{U}}{\partial{V}}} \right)_{\!T}}\right] \right\}_V$$

$$\ensuremath{\quad\quad \Rightarrow \quad\quad} \frac{1}{T} ... ...ensuremath{\frac{\partial{{}^2U}}{\partial{{T} \partial{V}}}}}$$

$$\ensuremath{\quad\quad \Rightarrow \quad\quad} \ensuremath{... ...\ensuremath{\frac{\partial{P}}{\partial{T}}} \right)_{\!V}}- P$$ (6)

Quest'ultima uguaglianza ci sarà molto utile nel seguito. Quando siamo interessati agli scambi di calore, le coordinate termodinamiche $T$ ed $S$ possono essere molto utili (le curve parametrizzate secondo queste due coordinate sono talvolta chiamate ``diagrammi $T$-$S$'').

Infatti, la quantità di calore assorbita da un sistema in una trasformazione infinitesima reversibile (area piccola tratteggiata in figura) è

$$\omega = T dS$$

Il calore scambiato in una trasformazione reversibile $\gamma$ da uno stato iniziale $i$ ad uno stato finale $f$ (area grande tratteggiata in figura) è:

$$Q = \int_{\gamma} \omega = \int_{S_i}^{S_f} T(S)\,dS$$

Trasformazione generale

In una trasformazione isoterma la temperatura è costante. In un diagramma $T$-$S$ una trasformazione isoterma è rappresentata da un segmento orizzontale; l'area sottesa dal segmento rappresenta il calore scambiato nella trasformazione fra gli stati $i$ ed $f$:

$$Q = \int_{S_i}^{S_f} T dS = T \int_{S_i}^{S_f} dS = T ( S_f - S_i ) = T \Delta S$$

Trasformazione isoterma

In una trasformazione adiabatica (detta anche isoentropica) l'entropia è costante. In un diagramma $T$-$S$ una trasformazione adiabatica corrisponde ad una linea verticale, ed ovviamente il calore scambiato è nullo:

$$S_i = S_F \ensuremath{\quad\quad \Rightarrow \quad\quad}Q = \int_{S_i}^{S_f} T dS = 0$$

Trasformazione adiabatica

In una trasformazione isocora (cioè a volume costante) abbiamo:

$$\left( \frac{\omega}{T} \right)_V = dS = \ensuremath{\left( \ensuremath{\frac{\partial{S}}{\partial{T}}} \right)_{\!V}}\,dT$$

Ma il calore somministrato per mole per unità di variazione di temperatura a volume costante non è altro che il calore specifico a volume costante $C_V$. Da ciò segue che

$$\ensuremath{\left( \ensuremath{\frac{\partial{S}}{\partial{... ...elineskip}{isocora~~}}}}}\quad}_{T_i}^{T_f} \frac{C_V}{T} \,dT$$

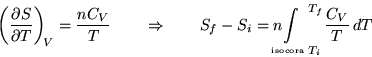
Questa relazione consente di calcolare la variazione di entropia $\Delta S$ nota la dipendenza di $C_V$ dalla temperatura. Se $C_V$ è costante, l'integrale vale

$$\Delta S = S_f - S_i = nC_V {{\int_{\makebox[0pt]{\textrm{... ...}}\quad}_{T_i}^{T_f} \frac{dT}{T} = n C_V \ln\frac{T_f}{T_i}$$

e la trasformazione corrispondente, nel piano $T$-$S$, è una esponenziale:

$$T(S) = e^{\frac{S}{nC_V}} + \textrm{cost}(V) \quad\quad \textrm{[isocora]}$$

Trasformazione isocora