La funzione energia interna

La funzione energia interna $U$ è una delle prime incontrate nello studio della termodinamica. Ora vogliamo però studiare la sua dipendenza dall'entropia. Combinando la prima e la seconda legge della termodinamica per trasformazioni reversibili otteniamo:

$$dU = \omega - P dV = T dS - P dV$$ (7)

Considerando $U$ come una funzione di $V$ ed $S$, otteniamo per confronto diretto che:

$$\ensuremath{\left( \ensuremath{\frac{\partial{U}}{\partial{... ...nsuremath{\frac{\partial{U}}{\partial{V}}} \right)_{\!S}}= - P$$

Le derivate parziali di $U$ soddisfano la condizione di Schwartz:

$$\left[ \ensuremath{\ensuremath{\frac{\partial{}}{\partial{V... ...ft( \ensuremath{\frac{\partial{P}}{\partial{S}}} \right)_{\!V}}$$ (8)

Questa relazione è la cosiddetta prima legge di Maxwell. Utilizzando le precedenti espressioni è facile determinare e ; basta infatti eseguire una misura di temperatura e una di pressione sul sistema. Come si determina invece ? In generale effettuare una misura di è difficile perchè bisogna determinare di quanto varia l'energia interna in seguito ad una variazione di volume mentre si somministra calore al sistema in modo da mantenere costante la temperatura. Conviene pertanto trovare una relazione che consenta di determinare sperimentalmente in modo più semplice. Abbiamo già dimostrato (vedere l'equazione 6) la seguente relazione:

$$\ensuremath{\left( \ensuremath{\frac{\partial{U}}{\partial{... ...\ensuremath{\frac{\partial{P}}{\partial{T}}} \right)_{\!V}}- P$$

è facilmente misurabile perchè rappresenta la variazione di pressione corrispondente ad una variazione di temperatura quando il volume viene mantenuto costante. Per un gas ideale la quantità $\ensuremath{\left( \ensuremath{\frac{\partial{U}}{\partial{V}}} \right)_{\!T}}$ si annulla esattamente:

$$P = \frac{nRT}{V} \ensuremath{\quad\quad \Rightarrow \quad... ...rtial{U}}{\partial{V}}} \right)_{\!T}}= T \frac{nR}{V} - P = 0$$

Questo è il ben noto risultato che l'energia interna di un gas perfetto è funzione della sola temperatura. In questo caso possiamo scrivere semplicemente:

$$dU = \ensuremath{\left( \ensuremath{\frac{\partial{U}}{\par... ...{T}}} \right)_{\!V}}dT \quad\quad \textrm{[per un gas ideale]}$$

ma la variazione di energia interna a volume costante (senza lavoro quindi) è la quantità di calore somministrata al sistema, dunque:

$$\ensuremath{\left( \ensuremath{\frac{\partial{U}}{\partial{... ... \ensuremath{\quad\quad \Rightarrow \quad\quad}dU = n C_V dT$$

Questo risultato viene ricavato anche da considerazioni puramente fenomenologiche (l'esperimento di Joule). Per un gas reale la situazione è differente, poichè la pressione non dipende più solo da $\frac{T}{V}$. Consideriamo l'equazione di stato di Van der Waals (vedere equazione 1):

$$P = \frac{nRT}{V-b} - \frac{a}{V^2} \ensuremath{\quad\quad... ...frac{\partial{P}}{\partial{T}}} \right)_{\!V}}= \frac{nR}{V-b}$$

quindi:

$$\ensuremath{\left( \ensuremath{\frac{\partial{U}}{\partial{V}}} \right)_{\!T}}= T \frac{nR}{V-b} - P = \frac{a}{V^2} > 0$$

Vediamo allora che, in un gas reale, a temperatura costante, all'aumentare del volume aumenta l'energia interna. Questo succede perchè aumenta la distanza media intermolecolare, perciò occorre fare un lavoro di allontanamento contro le forze di mutua attrazione delle molecole. Possiamo ricavare la dipendenza di $U$ da $V$ integrando lungo una trasformazione isoterma:

$$\ensuremath{\left( \ensuremath{\frac{\partial{U}}{\partial{... ...kip}{isoterma~~}}}}} \frac{a}{V^2} \,dV = - \frac{a}{V} + c(T)$$

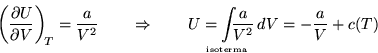
La costante di integrazione $c$ è indipendente da $V$ ma può ovviamente dipendere dalla temperatura dell'isoterma lungo la quale abbiamo integrato. La possiamo valutare considerando la variazione di $U$ rispetto a $T$, a $V$ costante (che abbiamo già detto essere il calore specifico $nC_V$):

$$n C_V = \ensuremath{\left( \ensuremath{\frac{\partial{U}}{\... ...uad\quad \Rightarrow \quad\quad} c(T) = nC_VT + \textrm{cost.}$$

Dunque, per un gas reale, l'energia interna, oltre a dipendere dalla temperatura, dipende anche dal volume occupato dal gas.