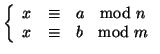
Se ![]() è una soluzione del sistema, allora gli elementi di
è una soluzione del sistema, allora gli elementi di
![]() sono tutte e sole le soluzioni del sistema (i.e. le soluzioni sono
tutte e sole della forma
sono tutte e sole le soluzioni del sistema (i.e. le soluzioni sono
tutte e sole della forma ![]() al variare di
al variare di
![]() ).
).
Dimostrazione.
Sia ![]() una soluzione del sistema allora esistono
una soluzione del sistema allora esistono
![]() tali che
tali che
![]() e quindi
e quindi ![]() . Ma allora dal fatto che
. Ma allora dal fatto che
![]() e
e
![]() si ha che
si ha che
![]() .
Viceversa, supponiamo che
.
Viceversa, supponiamo che
![]() , allora esistono
, allora esistono
![]() tali che
tali che
![]() . Ma allora
. Ma allora ![]() , detto quindi
, detto quindi
![]() , si ha
evidentemente che
, si ha
evidentemente che ![]() risolve entrambe le congruenze.
risolve entrambe le congruenze.
Sia
![]() risolve il sistema
risolve il sistema![]() . Dobbiamo provare
che se
. Dobbiamo provare
che se ![]() è una soluzione allora
è una soluzione allora
![]() .
.
![]() . Sia
. Sia ![]() un'altra soluzione, allora
un'altra soluzione, allora
![]() e
e
![]() e quindi sottraendo si ha
e quindi sottraendo si ha
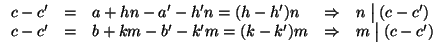
![]() . Sia
. Sia
![]() , ovvero
, ovvero
![]() . Dal fatto che
. Dal fatto che
![]() e che
e che
![]() segue che
segue che
![]() . In modo analogo si ha che
. In modo analogo si ha che
![]() e
quindi che
e
quindi che ![]() .
.
![]()

Dimostrazione.
Se ![]() è invertibile e
è invertibile e ![]() è un suo inverso, allora
è un suo inverso, allora
![]() ,
quindi esiste
,
quindi esiste ![]() tale che
tale che ![]() e quindi
e quindi ![]() , da cui
, da cui ![]() .
.
Viceversa, se ![]() allora esistono
allora esistono
![]() tali che
tali che
![]() , ma allora
, ma allora
![]() .
.
![]()
Dimostrazione. Dal fatto che ![]() in
in
![]() , moltiplicando entrambi i membri per
, moltiplicando entrambi i membri per ![]() , ed usando
le proprietà associativa, commutativa e dell'
, ed usando
le proprietà associativa, commutativa e dell'![]() si ottiene
si ottiene
Dimostrazione.
Se ![]() in
in
![]() allora
allora
![]() , se
, se ![]() in
in
![]() allora
esiste
allora
esiste ![]() tale che
tale che ![]() . Ma allora
. Ma allora
![]() è divisibile per
è divisibile per ![]() e quindi
e quindi ![]() in
in
![]() .
.
![]()
La proposizione 12.3 può allora essere rienunciata
Dimostrazione.
Se ![]() in
in
![]() allora
allora
![]() e quindi, dato che
e quindi, dato che ![]() è primo,
è primo,
![]() , da cui la tesi.
, da cui la tesi.
![]()