

Next: Moto dei satelliti
Up: Moto di una particella
Previous: Moto di una particella
Esplicitiamo ora 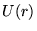 nella forma dell'energia potenziale gravitazionale
nella forma dell'energia potenziale gravitazionale
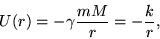 |
(6) |
dove 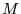 è la massa del centro di forza situato nell'origine
è la massa del centro di forza situato nell'origine 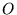 (vedere
figura 1). Per brevità è stato posto
(vedere
figura 1). Per brevità è stato posto 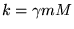 con
con
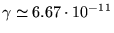 Nm
Nm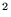 /kg
/kg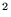 . In figura 2
è riportato il grafico dell'energia potenziale efficace
. In figura 2
è riportato il grafico dell'energia potenziale efficace
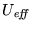 (equazione 5) per il potenziale gravitazionale
(equazione 5) per il potenziale gravitazionale 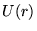 (equazione 6).
(equazione 6).
I risultati che troveremo per il potenziale gravitazionale potranno essere
estesi all'interazione coulombiana tra una carica 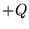 , centro di forza,
situata in
, centro di forza,
situata in 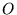 ed una carica di segno opposto
ed una carica di segno opposto 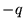 in moto relativo. Anche
in questo caso il potenziale è del tipo
in moto relativo. Anche
in questo caso il potenziale è del tipo 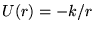 , dove però
, dove però
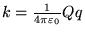 con
con
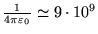 Nm
Nm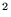 . Dall'equazione 4 possiamo
ricavare
. Dall'equazione 4 possiamo
ricavare
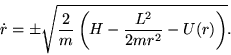 |
(7) |
Dei due segni prenderemo quello positivo; questa scelta corrisponde ad
imporre una condizione iniziale: il verso di rotazione della massa  .
.
Figura 2:
Grafico qualitativo del potenziale efficace nel caso
coulombiano attrattivo. Il potenziale centrifugo è positivo
e cresce come 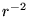 , mentre il potenziale coulombiano solo
come
, mentre il potenziale coulombiano solo
come 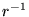 . Quindi per piccole distanze prevale l'effetto
centrifugo, per grandi quello coulombiano; a distanza intermedie
si forma allora una ``buca di potenziale''.
. Quindi per piccole distanze prevale l'effetto
centrifugo, per grandi quello coulombiano; a distanza intermedie
si forma allora una ``buca di potenziale''.
|
|
Poichè 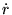 risulta solo funzione della variabile
risulta solo funzione della variabile 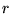 ,
al fine di ricavare
,
al fine di ricavare 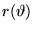 è sufficiente osservare che
è sufficiente osservare che
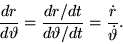 |
(8) |
Infatti, sostituendo le equazioni 2 e 7,
nonchè la legge dinamica 6, nella 8
si trova
Risolvendo rispetto a 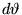 , dopo qualche semplice passaggio
algebrico si ottiene
, dopo qualche semplice passaggio
algebrico si ottiene
La formula precedente si semplifica notevolmente se raggruppiamo
le costanti del moto ponendo 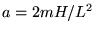 ,
, 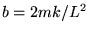 e
e 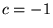 :
:
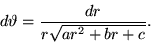 |
(9) |
Osserviamo che, poichè 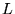 ed
ed 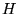 sono costanti,
sono costanti, 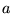 e
e 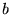 non dipendono
da
non dipendono
da 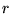 . Integrando entrambi i membri dell'equazione 9
(l'integrale del secondo membro si può trovare tabulato sulla maggior
parte delle tavole di integrali) si ottiene
. Integrando entrambi i membri dell'equazione 9
(l'integrale del secondo membro si può trovare tabulato sulla maggior
parte delle tavole di integrali) si ottiene
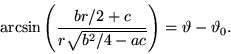 |
(10) |
La costante di integrazione  è determinata dalla posizione
angolare iniziale. Sostituendo nella soluzione 10 i valori
di
è determinata dalla posizione
angolare iniziale. Sostituendo nella soluzione 10 i valori
di  ,
,  e
e 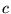 , dopo una semplice manipolazione algebrica e l'inversione
della funzione arcoseno, abbiamo
, dopo una semplice manipolazione algebrica e l'inversione
della funzione arcoseno, abbiamo
Risolvendo rispetto ad 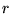 si ottiene la dipendenza di
si ottiene la dipendenza di 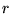 da
da 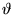 :
:
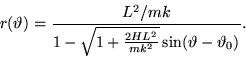 |
(11) |
Vogliamo ora riscrivere questa uguaglianza in una forma più semplice.
Calcoliamo il valore di 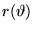 per
per
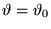 e
chiamiamolo
e
chiamiamolo 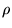 . Il seno si annulla ed otteniamo
. Il seno si annulla ed otteniamo
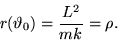 |
(12) |
Abbiamo visto che la conoscenza delle condizioni iniziali implica la
conoscenza di  e quindi di
e quindi di  . Siamo liberi di assumere il valore
iniziale
. Siamo liberi di assumere il valore
iniziale
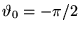 ; questo implica che
; questo implica che
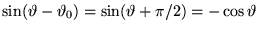 . Poniamo ancora
. Poniamo ancora
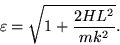 |
(13) |
In questo modo l'equazione 11 si riscrive come
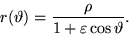 |
(14) |
Questa è l'equazione di una conica in coordinate polari.
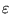 è detta eccentricità della conica. A decidere di
che tipo di conica si tratta è il valore di
è detta eccentricità della conica. A decidere di
che tipo di conica si tratta è il valore di 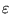 che, a sua
volta, è determinato da
che, a sua
volta, è determinato da 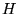 ed
ed 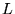 (equazione 13) e
quindi dalle condizioni iniziali. A questo punto può essere comodo
passare alle coordinate cartesiane; dalla figura 1
si deduce che
(equazione 13) e
quindi dalle condizioni iniziali. A questo punto può essere comodo
passare alle coordinate cartesiane; dalla figura 1
si deduce che
Sostituendo 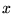 ed
ed 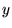 nell'equazione 14, considerando
che
nell'equazione 14, considerando
che
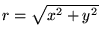 , dopo elementari manipolazioni, si trova
, dopo elementari manipolazioni, si trova
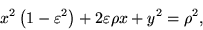 |
(15) |
che è l'equazione di una conica in coordinate cartesiane.
Esistono tre possibilità:
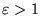 |
per le orbite iperboliche; |
 |
per le orbite paraboliche; |
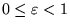 |
per le orbite ellittiche. |
Il caso  (cioè
(cioè  ed
ed
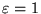 ) corrisponde ad
un'orbita rettilinea nella direzione del centro di forza: la particella
cade verso il centro di forza secondo una linea retta avente la stessa
direzione di
) corrisponde ad
un'orbita rettilinea nella direzione del centro di forza: la particella
cade verso il centro di forza secondo una linea retta avente la stessa
direzione di 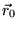 e
e 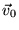 . Nel seguito escluderemo questa
possibilità.
. Nel seguito escluderemo questa
possibilità.
Orbite iperboliche:
nel caso che l'energia sia positiva ed il momento angolare non sia
nullo (cioè 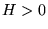 ed
ed 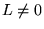 ) si ha
) si ha
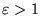 , ovvero
, ovvero
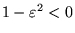 . Poniamo allora
. Poniamo allora
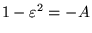 , con
, con
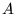 positivo; l'equazione 15 diventa
positivo; l'equazione 15 diventa
In questa equazione i coefficienti dei termini quadratici 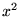 e
e 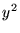 sono diversi e di segno opposto: si tratta dell'equazione di un'iperbole.
In figura 3-a) (tratto continuo) è riportato il grafico
di un'iperbole avente
sono diversi e di segno opposto: si tratta dell'equazione di un'iperbole.
In figura 3-a) (tratto continuo) è riportato il grafico
di un'iperbole avente
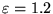 e
e 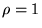 . Il centro di forza
è posto nell'origine.
. Il centro di forza
è posto nell'origine.
Orbite paraboliche:
nel caso che l'energia sia nulla ed il momento angolare non sia nullo
(cioè 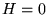 ed
ed 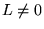 ) si ha
) si ha
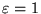 . In questo caso
l'equazione 15 diventa semplicemente
. In questo caso
l'equazione 15 diventa semplicemente
che è l'equazione di una parabola. In figura 3-a)
(tratteggio) è riportato il grafico di una parabola con
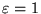 e
e 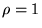 .
.
Orbite ellittiche e circolari:
nel caso che l'energia sia negativa ed il momento angolare non sia nullo
(cioè 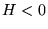 ed
ed 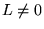 ) si ha
) si ha
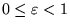 . In questo caso
l'equazione 15 assume la forma
. In questo caso
l'equazione 15 assume la forma
con
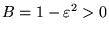 e
e
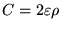 . In questa equazione
i coefficienti dei termini quadratici
. In questa equazione
i coefficienti dei termini quadratici 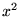 e
e 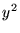 sono di ugual segno:
si tratta dell'equazione di un'ellisse. Nel caso in cui
sono di ugual segno:
si tratta dell'equazione di un'ellisse. Nel caso in cui
si ha esattamente
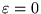 , e l'equazione 15
si riduce a quella di una circonferenza:
, e l'equazione 15
si riduce a quella di una circonferenza:
In figura 3-b) sono riportati i grafici di ellissi aventi
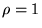 e differenti valori di
e differenti valori di 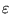 ; uno dei due fuochi è
nell'origine degli assi. Ad
; uno dei due fuochi è
nell'origine degli assi. Ad 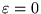 corrisponde l'orbita circolare
(curva tratteggiata a piccoli tratti), ad
corrisponde l'orbita circolare
(curva tratteggiata a piccoli tratti), ad
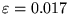 un'orbita con
la stessa eccentricità di quella terrestre (curva continua). Si osservi
come sia difficile distinguere l'orbita della terra dall'orbita circolare!
Ad
un'orbita con
la stessa eccentricità di quella terrestre (curva continua). Si osservi
come sia difficile distinguere l'orbita della terra dall'orbita circolare!
Ad
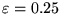 corrisponde un'orbita con la stessa eccentricità
di quella del pianeta Plutone (curva tratteggiata a tratti lunghi).
Nel sistema solare il pianeta con la più piccola eccentricità è
Nettuno (
corrisponde un'orbita con la stessa eccentricità
di quella del pianeta Plutone (curva tratteggiata a tratti lunghi).
Nel sistema solare il pianeta con la più piccola eccentricità è
Nettuno (
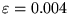 ) e quello con la più grande è Plutone.
) e quello con la più grande è Plutone.
Figura:
Parte a) sono rappresentate un iperbole (tratto
continuo,
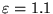 ) ed una parabola (tratteggiata,
) ed una parabola (tratteggiata,
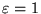 ). Parte b) sono rappresentate una
circonferenza (tratteggio fine,
). Parte b) sono rappresentate una
circonferenza (tratteggio fine, 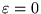 ), e due
ellissi con eccentricità diversa (tratto continuo,
), e due
ellissi con eccentricità diversa (tratto continuo,
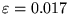 e tratteggio largo,
e tratteggio largo,
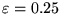 ).
Tutte queste coniche corrispondono all'equazione
).
Tutte queste coniche corrispondono all'equazione
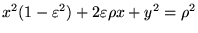 con
con 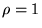 , quindi passano tutte per i punti
, quindi passano tutte per i punti 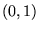 e
e 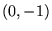 .
.
|
|
In figura 4-b sono riportate le orbite dei pianeti
esterni alla terra nel sistema solare e l'orbita della cometa Halley;
questa presenta un'eccentricità molto più alta di tutti i pianeti
del sistema solare (
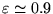 ).
).
I casi relativi alle possibili orbite del moto in un campo gravitazionale,
aventi stesso momento angolare 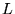 (quindi stesso valore per la
(quindi stesso valore per la 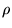 ,
vedere equazione 12) e diversa energia totale
,
vedere equazione 12) e diversa energia totale 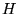 , sono
riassunti in figura 5 attraverso il diagramma
dell'energia potenziale efficace
, sono
riassunti in figura 5 attraverso il diagramma
dell'energia potenziale efficace
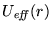 .
.


Next: Moto dei satelliti
Up: Moto di una particella
Previous: Moto di una particella
Stefano Bettelli
2002-04-21
![]() nella forma dell'energia potenziale gravitazionale
nella forma dell'energia potenziale gravitazionale
![]() , centro di forza,
situata in
, centro di forza,
situata in ![]() ed una carica di segno opposto
ed una carica di segno opposto ![]() in moto relativo. Anche
in questo caso il potenziale è del tipo
in moto relativo. Anche
in questo caso il potenziale è del tipo ![]() , dove però
, dove però
![]() con
con
![]() Nm
Nm![]() . Dall'equazione 4 possiamo
ricavare
. Dall'equazione 4 possiamo
ricavare
![\includegraphics[width=.7\textwidth]{ueff.eps}](img103.png)
![]() risulta solo funzione della variabile
risulta solo funzione della variabile ![]() ,
al fine di ricavare
,
al fine di ricavare ![]() è sufficiente osservare che
è sufficiente osservare che
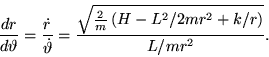
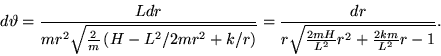
![]() è determinata dalla posizione
angolare iniziale. Sostituendo nella soluzione 10 i valori
di
è determinata dalla posizione
angolare iniziale. Sostituendo nella soluzione 10 i valori
di ![]() ,
, ![]() e
e ![]() , dopo una semplice manipolazione algebrica e l'inversione
della funzione arcoseno, abbiamo
, dopo una semplice manipolazione algebrica e l'inversione
della funzione arcoseno, abbiamo
![]() per
per
![]() e
chiamiamolo
e
chiamiamolo ![]() . Il seno si annulla ed otteniamo
. Il seno si annulla ed otteniamo
![]() (cioè
(cioè ![]() ed
ed
![]() ) corrisponde ad
un'orbita rettilinea nella direzione del centro di forza: la particella
cade verso il centro di forza secondo una linea retta avente la stessa
direzione di
) corrisponde ad
un'orbita rettilinea nella direzione del centro di forza: la particella
cade verso il centro di forza secondo una linea retta avente la stessa
direzione di ![]() e
e ![]() . Nel seguito escluderemo questa
possibilità.
. Nel seguito escluderemo questa
possibilità.
![]() ed
ed ![]() ) si ha
) si ha
![]() , ovvero
, ovvero
![]() . Poniamo allora
. Poniamo allora
![]() , con
, con
![]() positivo; l'equazione 15 diventa
positivo; l'equazione 15 diventa
![]() ed
ed ![]() ) si ha
) si ha
![]() . In questo caso
l'equazione 15 diventa semplicemente
. In questo caso
l'equazione 15 diventa semplicemente
![]() ed
ed ![]() ) si ha
) si ha
![]() . In questo caso
l'equazione 15 assume la forma
. In questo caso
l'equazione 15 assume la forma
![]() e differenti valori di
e differenti valori di ![]() ; uno dei due fuochi è
nell'origine degli assi. Ad
; uno dei due fuochi è
nell'origine degli assi. Ad ![]() corrisponde l'orbita circolare
(curva tratteggiata a piccoli tratti), ad
corrisponde l'orbita circolare
(curva tratteggiata a piccoli tratti), ad
![]() un'orbita con
la stessa eccentricità di quella terrestre (curva continua). Si osservi
come sia difficile distinguere l'orbita della terra dall'orbita circolare!
Ad
un'orbita con
la stessa eccentricità di quella terrestre (curva continua). Si osservi
come sia difficile distinguere l'orbita della terra dall'orbita circolare!
Ad
![]() corrisponde un'orbita con la stessa eccentricità
di quella del pianeta Plutone (curva tratteggiata a tratti lunghi).
Nel sistema solare il pianeta con la più piccola eccentricità è
Nettuno (
corrisponde un'orbita con la stessa eccentricità
di quella del pianeta Plutone (curva tratteggiata a tratti lunghi).
Nel sistema solare il pianeta con la più piccola eccentricità è
Nettuno (
![]() ) e quello con la più grande è Plutone.
) e quello con la più grande è Plutone.
![\includegraphics[width=.45\textwidth]{iperparab.eps}](img151.png)
![\includegraphics[width=.45\textwidth]{ellissi.eps}](img152.png)
![]() ).
).
![]() (quindi stesso valore per la
(quindi stesso valore per la ![]() ,
vedere equazione 12) e diversa energia totale
,
vedere equazione 12) e diversa energia totale ![]() , sono
riassunti in figura 5 attraverso il diagramma
dell'energia potenziale efficace
, sono
riassunti in figura 5 attraverso il diagramma
dell'energia potenziale efficace
![]() .
.