

Next: About this document ...
Up: Moto di una particella
Previous: Moto in un potenziale
Figura:
Parte a
Sono mostrate le diverse orbite per satelliti terrestri
corrispondenti ai casi 1, 2 e 3 di figura 5.
La curva 1 corrisponde al caso 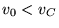 , in cui la posizione
iniziale
, in cui la posizione
iniziale 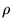 (equazione 12) coincide con l'afelio.
La curva 2 corrisponde al moto circolare.
La curva 3 corrisponde al caso
(equazione 12) coincide con l'afelio.
La curva 2 corrisponde al moto circolare.
La curva 3 corrisponde al caso
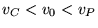 , in cui la
posizione iniziale
, in cui la
posizione iniziale 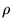 (equazione 12) coincide
con il perielio.
In tutti e tre i casi il valore di
(equazione 12) coincide
con il perielio.
In tutti e tre i casi il valore di 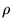 e quindi del momento
angolare è fissato.
Parte b Sono rappresentate le orbite dei pianeti del
sistema solare esterni alla Terra, assieme alla cometa Halley,
che presenta una eccentricità molto maggiore.
e quindi del momento
angolare è fissato.
Parte b Sono rappresentate le orbite dei pianeti del
sistema solare esterni alla Terra, assieme alla cometa Halley,
che presenta una eccentricità molto maggiore.
|
|
Le conclusioni precedenti possono essere applicate anche ai satelliti di
un pianeta; in questo caso il pianeta gioca il ruolo di centro della forza.
Supponiamo di voler lanciare in orbita attorno alla Terra un satellite,
ad una distanza 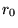 dal centro della Terra. La velocità iniziale del
satellite
dal centro della Terra. La velocità iniziale del
satellite 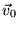 sia diretta ortogonalmente al raggio vettore
sia diretta ortogonalmente al raggio vettore
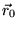 che ne individua la posizione iniziale. Ci chiediamo quale
deve essere il valore di
che ne individua la posizione iniziale. Ci chiediamo quale
deve essere il valore di 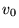 affinché il satellite percorra un'orbita
circolare e quale il valor minimo di
affinché il satellite percorra un'orbita
circolare e quale il valor minimo di 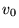 affinché esso abbandoni
per sempre la Terra.
affinché esso abbandoni
per sempre la Terra.
Orbita circolare:
la condizione per l'orbita circolare si ricava dalla seconda legge di
Newton, imponendo che l'accelerazione gravitazionale eguagli quella
centrifuga. Indicando con 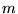 la massa del satellite, con
la massa del satellite, con 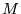 quella
della Terra e con
quella
della Terra e con 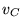 il valore di
il valore di 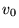 determinato da questa
uguaglianza, si ha
determinato da questa
uguaglianza, si ha
Orbita parabolica:
la minima velocità iniziale 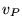 che vedrebbe la massa
che vedrebbe la massa 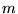 allontanarsi
per sempre dalla Terra è quella che dà luogo ad un'orbita parabolica.
Essa si ottiene imponendo che l'energia meccanica
allontanarsi
per sempre dalla Terra è quella che dà luogo ad un'orbita parabolica.
Essa si ottiene imponendo che l'energia meccanica 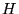 sia nulla:
sia nulla:
Il valore 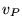 corrisponde alla velocità di fuga a partire dalla quota
corrisponde alla velocità di fuga a partire dalla quota
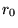 . Se
. Se 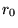 coincidesse con il raggio della Terra
coincidesse con il raggio della Terra 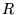 , si avrebbe
, si avrebbe
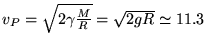 Km/s.
È interessante domandarsi ora quale sia il tipo di orbita per
velocità
Km/s.
È interessante domandarsi ora quale sia il tipo di orbita per
velocità 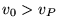 e per
e per 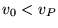 .
.
Orbite iperboliche ed ellittiche:
per 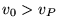 si ha che l'energia è positiva e quindi che le orbite
sono di tipo iperbolico (figura 5). Abbiamo trovato
che l'energia meccanica è nulla per
si ha che l'energia è positiva e quindi che le orbite
sono di tipo iperbolico (figura 5). Abbiamo trovato
che l'energia meccanica è nulla per 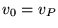 (orbita parabolica)
mentre per
(orbita parabolica)
mentre per
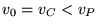 (orbita circolare) si ha che
(orbita circolare) si ha che
In generale per 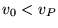 si ha
si ha 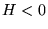 ; ad energie meccaniche negative
corrispondono sempre orbite chiuse (figura 5),
quindi per
; ad energie meccaniche negative
corrispondono sempre orbite chiuse (figura 5),
quindi per
il satellite percorre orbite ellittiche. In particolare, per 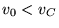 ,
il satellite si muove su orbite aventi l'afelio coincidente con la
posizione iniziale
,
il satellite si muove su orbite aventi l'afelio coincidente con la
posizione iniziale 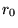 (vedi figura 5 curva 1,
parte spessa) mentre e per
(vedi figura 5 curva 1,
parte spessa) mentre e per
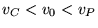 il satellite percorre orbite
ellittiche con la posizione iniziale coincidente con il perielio (vedi
figura 5 curva 3, parte spessa). In figura
5 sono mostrate le curve di energia potenziale
efficace
il satellite percorre orbite
ellittiche con la posizione iniziale coincidente con il perielio (vedi
figura 5 curva 3, parte spessa). In figura
5 sono mostrate le curve di energia potenziale
efficace
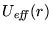 (vedere anche la figura 2) ottenute
per i differenti valori di
(vedere anche la figura 2) ottenute
per i differenti valori di 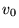 . Al crescere di
. Al crescere di 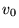 e quindi di
e quindi di
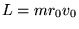 , l'energia centrifuga
, l'energia centrifuga
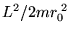 aumenta mentre
aumenta mentre
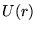 resta invariata; ne consegue che le curve del potenziale efficace
resta invariata; ne consegue che le curve del potenziale efficace
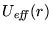 si spostano verso l'alto. Ad ogni curva corrisponde una
diversa traiettoria: alla curva
si spostano verso l'alto. Ad ogni curva corrisponde una
diversa traiettoria: alla curva 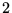 , corrisponde la traiettoria circolare,
alla curva
, corrisponde la traiettoria circolare,
alla curva 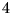 quella parabolica, alle curve
quella parabolica, alle curve 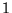 e
e 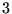 traiettorie
ellittiche e alla curva
traiettorie
ellittiche e alla curva 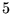 quella iperbolica. Le diverse orbite sono
riportate in figura 4-a.
quella iperbolica. Le diverse orbite sono
riportate in figura 4-a.
Figura:
Moto dei satelliti:
Curva 1 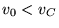 , moto ellittico, la posizione
iniziale
, moto ellittico, la posizione
iniziale 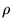 (equazione 12) coincide con
l'afelio (linea magenta in grassetto), ellisse a
nella figura 4-a.
Curva 2
(equazione 12) coincide con
l'afelio (linea magenta in grassetto), ellisse a
nella figura 4-a.
Curva 2 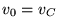 , moto circolare.
Curva 3
, moto circolare.
Curva 3
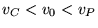 , moto ellittico, la
posizione iniziale
, moto ellittico, la
posizione iniziale 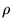 (equazione 12)
coincide con il perielio (linea magenta in grassetto),
ellisse b nella figura 4-a.
Curva 4
(equazione 12)
coincide con il perielio (linea magenta in grassetto),
ellisse b nella figura 4-a.
Curva 4 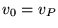 , moto parabolico.
Curva 5
, moto parabolico.
Curva 5 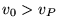 , moto iperbolico.
, moto iperbolico.
I segmenti orizzontali tratteggiati rappresentano l'energia
totale 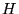 , essi sono numerati da
, essi sono numerati da 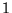 a
a 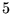 come le corrispondenti
curve di energia potenziale efficace; il segmento numero
come le corrispondenti
curve di energia potenziale efficace; il segmento numero 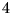 (moto
parabolico) coincide con l'asse delle ascisse,
(moto
parabolico) coincide con l'asse delle ascisse, 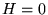 . In tutti
i casi il valore di
. In tutti
i casi il valore di 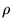 e quindi del momento angolare è fissato.
e quindi del momento angolare è fissato.
|
|


Next: About this document ...
Up: Moto di una particella
Previous: Moto in un potenziale
Stefano Bettelli
2002-04-21
![\includegraphics[width=.35\textwidth]{orbite.eps}](img155.png)
![\includegraphics[width=.35\textwidth]{sistsolare.eps}](img156.png)
![\includegraphics[width=.35\textwidth]{orbite.eps}](img155.png)
![\includegraphics[width=.35\textwidth]{sistsolare.eps}](img156.png)
![]() dal centro della Terra. La velocità iniziale del
satellite
dal centro della Terra. La velocità iniziale del
satellite ![]() sia diretta ortogonalmente al raggio vettore
sia diretta ortogonalmente al raggio vettore
![]() che ne individua la posizione iniziale. Ci chiediamo quale
deve essere il valore di
che ne individua la posizione iniziale. Ci chiediamo quale
deve essere il valore di ![]() affinché il satellite percorra un'orbita
circolare e quale il valor minimo di
affinché il satellite percorra un'orbita
circolare e quale il valor minimo di ![]() affinché esso abbandoni
per sempre la Terra.
affinché esso abbandoni
per sempre la Terra.
![]() la massa del satellite, con
la massa del satellite, con ![]() quella
della Terra e con
quella
della Terra e con ![]() il valore di
il valore di ![]() determinato da questa
uguaglianza, si ha
determinato da questa
uguaglianza, si ha
![]() che vedrebbe la massa
che vedrebbe la massa ![]() allontanarsi
per sempre dalla Terra è quella che dà luogo ad un'orbita parabolica.
Essa si ottiene imponendo che l'energia meccanica
allontanarsi
per sempre dalla Terra è quella che dà luogo ad un'orbita parabolica.
Essa si ottiene imponendo che l'energia meccanica ![]() sia nulla:
sia nulla:
![]() si ha che l'energia è positiva e quindi che le orbite
sono di tipo iperbolico (figura 5). Abbiamo trovato
che l'energia meccanica è nulla per
si ha che l'energia è positiva e quindi che le orbite
sono di tipo iperbolico (figura 5). Abbiamo trovato
che l'energia meccanica è nulla per ![]() (orbita parabolica)
mentre per
(orbita parabolica)
mentre per
![]() (orbita circolare) si ha che
(orbita circolare) si ha che
![\includegraphics[width=.8\textwidth]{motosatelliti.eps}](img173.png)